题目内容
9.已知曲线y=x2,求过点P(2,1)的切线方程.分析 设出切点,求出导数,求得切线的斜率和方程,代入点(2,1),解方程可得切点,进而得到所求切线的方程.
解答 解:设切点为(m,m2),
y=x2的导数为y′=2x,
即有切线的斜率为k=2m,
切线的方程为y-m2=2m(x-m),
代入(2,1),可得1-m2=2m(2-m),
解得m=2±$\sqrt{3}$,
即有过点P(2,1)的切线方程为
y-1=2(2±$\sqrt{3}$)(x-2),
即为y=(4+2$\sqrt{3}$)x-7-4$\sqrt{3}$,或y=(4-2$\sqrt{3}$)x-7+4$\sqrt{3}$.
点评 本题考查导数的运用:求切线的方程,注意确定切点,考查导数的几何意义,直线方程的运用,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
20.已知空间中四个不共面的点O、A、B、C,若|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,且cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=cos<$\overrightarrow{OA}$,$\overrightarrow{OC}$>,则sin<$\overrightarrow{OA}$,$\overrightarrow{BC}$>的值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
17.如图,若下列程序执行的结果是2,则输入的x值是( )


| A. | 2 | B. | -2 | C. | 2或-2 | D. | 0 |
14.$\root{3}{(lg5-1)^{3}}$-$\sqrt{(lg2-1)^{2}}$=( )
| A. | lg$\frac{2}{5}$ | B. | 1 | C. | -1 | D. | lg$\frac{5}{2}$ |
1.将函数y=sinx的图象向左平移φ(0≤φ≤2π)个单位后,得到函数$y=sin(x-\frac{π}{6})$的图象,则φ=( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{7π}{6}$ | D. | $\frac{11π}{6}$ |
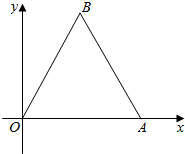 正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.
正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.