题目内容
7.已知函数f(x)=-x4+4x3-ax2+1在区间[0,1]上单调递减,在区间[1,2]上单调递增.(1)求a的值;
(2)记g(x)=1-bx2,若方程f(x)=g(x)的解集恰有3个元素,求b的取值范围.
分析 (1)可求导数,f′(x)=-4x3+12x2-2ax,而根据题意知x=1为f(x)的极值点,从而有f′(1)=0,这样即可求出a=4;
(2)由方程f(x)=g(x)可整理得到x2(x2-4x+4-b)=0,从而由题意得到一元二次方程x2-4x+4-b=0有两个不等的非零实根,从而有$\left\{\begin{array}{l}{△>0}\\{4-b≠0}\end{array}\right.$,解该不等式组便可得出b的取值范围.
解答 解:(1)f′(x)=-4x3+12x2-2ax;
∵函数f(x)在[0,1]上单调递减,在[1,2]上单调递增;
∴x=1是f(x)的极值点;
f′(1)=0,即-4•13+12•12-2a•1=0;
解得a=4;
(2)由f(x)=g(x)整理可得x2(x2-4x+4-b)=0;
由题意知此方程有三个不相等的实数根,又x=0为方程的一实数根;
则方程x2-4x+4-b=0应有两个不相等的非零实根;
∴△>0,且4-b≠0,即(-4)2-4(4-b)>0且b≠4;
解得b>0且b≠4;
∴b的取值范围是(0,4)∪(4,+∞).
点评 考查利用导数研究函数的单调性和极值,函数极值的概念,根的存在性及根的个数判断,以及一元二次方程实根个数和判别式△取值的关系.

练习册系列答案
相关题目
17.如图,若下列程序执行的结果是2,则输入的x值是( )


| A. | 2 | B. | -2 | C. | 2或-2 | D. | 0 |
15.命题“若x<3,则x2≤9”的逆否命题是( )
| A. | 若x≥3,则x2>9 | B. | 若x2≤9,则x<3 | C. | 若x2>9,则x≥3 | D. | 若x2≥9,则x>3 |
12.一首小诗《数灯》,诗曰:“远望灯塔高7层,红光点点倍加增,顶层数来有4盏,塔上共有多少灯?”答曰( )
| A. | 252 盏 | B. | 256盏 | C. | 508 盏 | D. | 512盏 |
16.如图所示空间直角坐标系中,右手空间直角坐标系的个数为( )

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
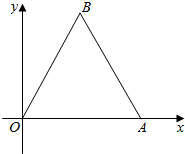 正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.
正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.