题目内容
16.如图在平行四边形ABCD中,已知AB=8,AD=5,$\overrightarrow{CP}$=3$\overrightarrow{PD}$,$\overrightarrow{AP}$•$\overrightarrow{BP}$=2,则$\overrightarrow{AB}$•$\overrightarrow{AD}$的值是( )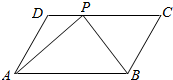
| A. | 18 | B. | 20 | C. | 22 | D. | 24 |
分析 由$\overrightarrow{CP}$=3$\overrightarrow{PD}$,可得$\overrightarrow{AP}$=$\overrightarrow{AD}$+$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{BP}$=$\overrightarrow{AD}$-$\frac{3}{4}$$\overrightarrow{AB}$,进而由AB=8,AD=5,$\overrightarrow{CP}$=3$\overrightarrow{PD}$,$\overrightarrow{AP}$•$\overrightarrow{BP}$=2,构造方程,进而可得答案.
解答 解:∵$\overrightarrow{CP}$=3$\overrightarrow{PD}$,
∴$\overrightarrow{AP}$=$\overrightarrow{AD}$+$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{BP}$=$\overrightarrow{AD}$-$\frac{3}{4}$$\overrightarrow{AB}$,
又∵AB=8,AD=5,
∴$\overrightarrow{AP}$•$\overrightarrow{BP}$=($\overrightarrow{AD}$+$\frac{1}{4}$$\overrightarrow{AB}$)•($\overrightarrow{AD}$-$\frac{3}{4}$$\overrightarrow{AB}$)=|$\overrightarrow{AD}$|2-$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AD}$-$\frac{3}{16}$|$\overrightarrow{AB}$|2=25-$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AD}$-12=2,
故$\overrightarrow{AB}$•$\overrightarrow{AD}$=22,
故答案为:22.
点评 本题考查的知识点是向量在几何中的应用,平面向量数量积的运算,其中根据已知得到$\overrightarrow{AP}$=$\overrightarrow{AD}$+$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{BP}$=$\overrightarrow{AD}$-$\frac{3}{4}$$\overrightarrow{AB}$,是解答的关键.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{8}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
| A. | 只能是x=-1 | |
| B. | 可能是y轴 | |
| C. | 可能在y轴右侧且在直线x=2的左侧 | |
| D. | 可能在y轴左侧且在直线x=-2的右侧 |