题目内容
15.在△ABC中,已知a=8,b=7,c=3,则B=60°.分析 根据题意,由a、b、c的长,结合余弦定理可得,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{64+9-49}{2×8×3}$=$\frac{24}{48}$=$\frac{1}{2}$,进而由B的范围可得B的大小,即可得答案.
解答 解:根据题意,在△ABC中,a=8,b=7,c=3,
cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{64+9-49}{2×8×3}$=$\frac{24}{48}$=$\frac{1}{2}$,
而0°<B<180°,
则B=60°,
故答案为:60°.
点评 本题考查余弦定理的运用,关键是熟悉余弦定理的内容并熟练运用.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
3.已知tanαcosα>0且cotαsinα<0,则α是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.f(x)=xcosx-5sinx+2,若f(2)=7,则f(-2)的值为( )
| A. | -7 | B. | 9 | C. | -5 | D. | -3 |
7.函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(-$\frac{π}{2}$)=( )
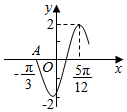
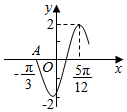
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
4.设向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$$+\overrightarrow{b}$$+\overrightarrow{c}$=$\overrightarrow{0}$,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=4,则$\overrightarrow{a}$$•\overrightarrow{b}$=( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |