题目内容
6.如图,网格纸上小正方形边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体表面积为( )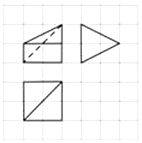
| A. | $10+\sqrt{5}$ | B. | $7+3\sqrt{5}$ | C. | $8+\sqrt{5}$ | D. | 8 |
分析 根据三视图得出空间几何体是镶嵌在正方体中的四棱锥O-ABCD,正方体的棱长为2,A,D为棱的中点,利用球的几何性质求解即可.
解答 解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O-ABCD,
正方体的棱长为2,A,D为棱的中点
底面ABCD的面积为:2×$\sqrt{{2}^{2}+{1}^{2}}$=2$\sqrt{5}$,
侧面△OCD的面积为:$\frac{1}{2}$×2×2=2,
侧面△OBC的面积为:$\frac{1}{2}$×2×2=2,
侧面△OAD的面积为:$\frac{1}{2}$×2×$\sqrt{5}$=$\sqrt{5}$,
侧面△OAB的面积为:$\sqrt{\frac{3+\sqrt{5}+2\sqrt{2}}{2}•\frac{-3+\sqrt{5}+2\sqrt{2}}{2}•\frac{3-\sqrt{5}+2\sqrt{2}}{2}•\frac{3+\sqrt{5}-2\sqrt{2}}{2}}$=3,
故表面积S=7+3$\sqrt{5}$,
故选:B
点评 本题考查的知识点是棱锥的几何特征,简单几何体的三视图,求侧面△OAB的面积难度较大.

练习册系列答案
相关题目
18.已知点A($\sqrt{3}$,2),B(0,3),C(0,1),则∠BAC=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
16.当双曲线M:$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{2m+4}$=1(-2<m<0)的焦距取得最小值时,双曲线M的渐近线方程为( )
| A. | y=±$\sqrt{2}x$ | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±2x | D. | y=±$\frac{1}{2}$x |