题目内容
1.在非等腰三角形ABC中,∠A,∠B,∠C所对的边分别为a,b,c,若a,b,2c成等比数列,3a2,b2,3c2成等差数列,则cosB=-$\frac{1}{3}$.分析 分别利用等比数列及等差数列的中项的性质列出关系式,再由余弦定理,即可得到所求值.
解答 解:由a,b,2c成等比数列,3a2,b2,3c2成等差数列
可得:b2=2ac,2b2=3a2+3c2,即a2+c2=$\frac{2}{3}$b2,
∴由余弦定理得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\frac{2}{3}{b}^{2}-{b}^{2}}{{b}^{2}}$=-$\frac{1}{3}$.
故答案为:-$\frac{1}{3}$.
点评 此题考查了余弦定理,等比数列、等差数列的中项的性质,考查运算能力,熟练掌握定理及性质是解本题的关键.

练习册系列答案
相关题目
8.定义域为R的偶函数f(x)满足?x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(x+1)恰有三个零点,则a的取值范围是( )
| A. | (0,$\frac{\sqrt{5}}{5}$) | B. | (0,$\frac{\sqrt{3}}{3}$) | C. | ($\frac{\sqrt{5}}{5}$,$\frac{\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{6}}{6}$,$\frac{\sqrt{5}}{5}$) |
9.对于函数f(x)=$\frac{x-1}{x+1}$,设函数f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N+,n≥2),令集合M={x|f2016(x)=x,x∈R},则集合M为( )
| A. | 空集 | B. | 实数集 | C. | 单元素集 | D. | 二元素集 |
16.若集合M={1,2},N={2,3},则集合M∪N真子集的个数是.( )
| A. | 7 | B. | 8 | C. | 15 | D. | 16 |
6.如图,网格纸上小正方形边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体表面积为( )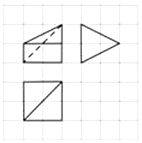

| A. | $10+\sqrt{5}$ | B. | $7+3\sqrt{5}$ | C. | $8+\sqrt{5}$ | D. | 8 |
10.某中学是走读中学,为了让学生更有效率利用下午放学后的时间,学校在本学期第一次月考后设立了多间自习室,以便让学生在自习室自主学习、完成作业,同时每天派老师轮流值班.在本学期第二次月考后,高一某班数学老师统计了两次考试该班数学成绩优良人数和非优良人数,得到如下2×2列联表:
(1)能否在在犯错误的概率不超过0.005的前提下认为设立自习室对提高学生成绩有效;
(2)设从该班第一次月考的所有学生的数学成绩中任取2个,取到优良成绩的个数为X,从该班第二次月考的所有学生的数学成绩中任取2个,取到优良成绩的个数为Y,求X与Y的期望并比较大小,请解释所得结论的实际意义.
下面的临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 非优良 | 优良 | 总计 | |
| 未设立自习室 | 25 | 15 | 40 |
| 设立自习室 | 10 | 30 | 40 |
| 总计 | 35 | 45 | 80 |
(2)设从该班第一次月考的所有学生的数学成绩中任取2个,取到优良成绩的个数为X,从该班第二次月考的所有学生的数学成绩中任取2个,取到优良成绩的个数为Y,求X与Y的期望并比较大小,请解释所得结论的实际意义.
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |