题目内容
14.已知函数f(x)=-2sin2x+2$\sqrt{3}$sinxcosx+1(Ⅰ)求f(x)的最小正周期及对称中心
(Ⅱ)若x∈[-$\frac{π}{6}$,$\frac{π}{3}$],求f(x)的最大值和最小值.
分析 (1)利用二倍角以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,即可求周期和对称中心.
(2)x∈[-$\frac{π}{6}$,$\frac{π}{3}$]时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的取值最大和最小值.
解答 解:(1)函数f(x)=-2sin2x+2$\sqrt{3}$sinxcosx+1,
化简可得:f(x)=cos2x-1+$\sqrt{3}$sin2x+1
=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$).
∴f(x)的最小正周期T=$\frac{2π}{2}=π$,
由2x+$\frac{π}{6}$=kπ(k∈Z)可得对称中心的横坐标为x=$\frac{1}{2}$kπ$-\frac{π}{12}$
∴对称中心($\frac{1}{2}$kπ$-\frac{π}{12}$,0),(k∈Z).
(2)当x∈[-$\frac{π}{6}$,$\frac{π}{3}$]时,2x+$\frac{π}{6}$∈[$-\frac{π}{6}$,$\frac{5π}{6}$]
当2x+$\frac{π}{6}$=$-\frac{π}{6}$时,函数f(x)取得最小值为$-\frac{1}{2}×2=-1$.
当2x+$\frac{π}{6}$=$\frac{π}{2}$时,函数f(x)取得最大值为2×1=2.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
2.已知单位圆有一条长为$\sqrt{2}$的弦AB,动点P在圆内,则使得$\overrightarrow{AP}$$•\overrightarrow{AB}$≥2的概率为( )
| A. | $\frac{π-2}{4π}$ | B. | $\frac{π-2}{π}$ | C. | $\frac{3π-2}{4π}$ | D. | $\frac{2}{π}$ |
9.对于函数f(x)=$\frac{x-1}{x+1}$,设函数f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N+,n≥2),令集合M={x|f2016(x)=x,x∈R},则集合M为( )
| A. | 空集 | B. | 实数集 | C. | 单元素集 | D. | 二元素集 |
6.如图,网格纸上小正方形边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体表面积为( )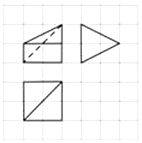

| A. | $10+\sqrt{5}$ | B. | $7+3\sqrt{5}$ | C. | $8+\sqrt{5}$ | D. | 8 |