题目内容
若数列{an}的通项公式为an=1+
(n∈N*),{an}的最大项为第x项,最小项为第y项,则x+y的值( )
| 2 |
| 2n-7 |
| A、5 | B、6 | C、7 | D、8 |
考点:数列的应用
专题:计算题
分析:由题设条件知,a1>a2>a3,且a4>a5>a6>0,再由a1=
,a2=
,a3=-1,a4=3,故a3为最小项,a4为最大项,由此可求出x+y的值.
| 3 |
| 5 |
| 1 |
| 3 |
解答:
解:由函数f(n)=1+
(n∈N*)的单调性知,
a1>a2>a3,且a4>a5>a6>0,
又a1=
,a2=
,a3=-1,a4=3,故a3为最小项,a4为最大项,
∴x+y的值为7.
故选C.
| 2 |
| 2n-7 |
a1>a2>a3,且a4>a5>a6>0,
又a1=
| 3 |
| 5 |
| 1 |
| 3 |
∴x+y的值为7.
故选C.
点评:本题考查数列的性质,解题时注意公式的灵活运用.

练习册系列答案
相关题目
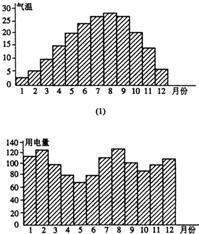 一般地,家庭用电量y(千瓦)与气温x(℃)有函数关系y=f(x).图(1)表示某年12月中每月的平均气温,图(2)表示某家庭在12个月中每月的用电量.试在数集A={x|5≤x≤30,x是2.5的整数倍}中确定一个最小值x1和最大值x2,使y=f(x)是[x1,x2]上的增函数,则区间[x1,x2]=
一般地,家庭用电量y(千瓦)与气温x(℃)有函数关系y=f(x).图(1)表示某年12月中每月的平均气温,图(2)表示某家庭在12个月中每月的用电量.试在数集A={x|5≤x≤30,x是2.5的整数倍}中确定一个最小值x1和最大值x2,使y=f(x)是[x1,x2]上的增函数,则区间[x1,x2]=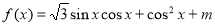 ,
,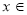
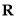 .
. 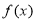 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 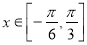 时,
时,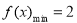 ,求函数
,求函数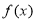 的最大值,并指出
的最大值,并指出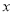 取何值时,函数
取何值时,函数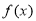 取得最大值.
取得最大值.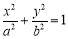 (a>b>0)的上顶点为A,左,右焦点分别为F1,F2,且椭圆C过点P(
(a>b>0)的上顶点为A,左,右焦点分别为F1,F2,且椭圆C过点P(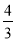 ,
,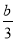 ),以AP为直径的圆恰好过右焦点F2.
),以AP为直径的圆恰好过右焦点F2.
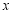 轴上是否存在两定点,使其到直线l的距离之积为1?若存在,请求出两定点坐标;若不存在,请说明理由.
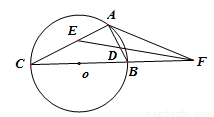
轴上是否存在两定点,使其到直线l的距离之积为1?若存在,请求出两定点坐标;若不存在,请说明理由.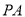 与圆
与圆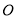 相切于点
相切于点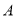 ,经过点
,经过点 的割线
的割线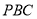 交圆
交圆 于点
于点 和点
和点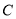 ,
,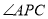 的平分线分别交AB、AC于点
的平分线分别交AB、AC于点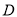 和
和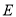 .
.
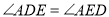 ;
;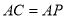 ,求
,求 的值.
的值.