题目内容
(本小题满分10分))【选修4—1:几何证明选讲】
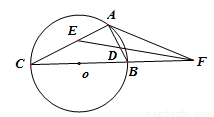
已知直线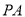 与圆
与圆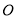 相切于点
相切于点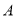 ,经过点
,经过点 的割线
的割线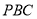 交圆
交圆 于点
于点 和点
和点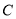 ,
,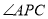 的平分线分别交AB、AC于点
的平分线分别交AB、AC于点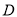 和
和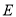 .
.
(1)证明: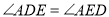 ;
;
(2)若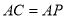 ,求
,求 的值.
的值.
(1)
 为
为 的平分线,
的平分线,
 ;
;
又 直线
直线 是圆
是圆 的切线,
的切线, ;
;
又
 ,
, ;
;

 . 5分
. 5分
(2)过 作
作 于
于 ;
;

 为圆
为圆 的直径,
的直径, ,又
,又
由 ,则
,则 ,
,
而 ,
,
 ;则
;则 ,
,
得 ,
,
所求即 . 10分
. 10分
【解析】
试题分析(1)根据弦切角定理,得到∠BAP=∠C,结合PE平分∠APC,可得∠BAP+∠APD=∠C+∠CPE,最后用三角形的外角可得∠ADE=∠AED;
(2)根据AC=AP得到∠APC=∠C,结合(1)中的结论可得∠APC=∠C=∠BAP,再在△APC中根据直径BC得到∠PAC=90°+∠BAP,利用三角形内角和定理可得 .利用直角三角形中正切的定义,得到
.利用直角三角形中正切的定义,得到 ,最后通过内角相等证明出△APC∽△BPA,从而
,最后通过内角相等证明出△APC∽△BPA,从而 .
.
考点:弦切角;相似三角形的性质

练习册系列答案
相关题目
 集合
集合
 则
则 为_________________.
为_________________. q为真命题,则p
q为真命题,则p q为真命题。
q为真命题。 ”是“
”是“ ”的充分不必要条件。
”的充分不必要条件。 x∈R,使得x
x∈R,使得x +x-1<0,则
+x-1<0,则 p :
p : x∈R,使得x
x∈R,使得x ,则x=1或x=2”的逆否命题为“若x
,则x=1或x=2”的逆否命题为“若x 1或x
1或x 2,则
2,则 ”。
”。
 .
. 的单调递增区间;
的单调递增区间;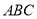 中,a、b、c分别是角A、B、C的对边,若
中,a、b、c分别是角A、B、C的对边,若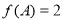 ,
, ,
, 的面积为
的面积为 ,求
,求 的值.
的值. 为不等式组
为不等式组 ,表示的平面区域上的一点,则
,表示的平面区域上的一点,则 的取值范围为
的取值范围为 B.
B. C.
C. D.
D.
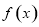 是定义在
是定义在 上恒不为零的函数,且对任意的实数
上恒不为零的函数,且对任意的实数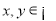 ,都有
,都有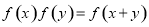 ,若
,若 ,
, ,则数列
,则数列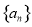 的前
的前 项和
项和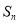 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
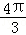 B.π C.
B.π C.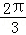 D.
D.