题目内容
设函数f(x)=ax2-(a+1)x+1.
(1)若f(x)为偶函数,求实数a的值;
(2)若a∈[-1,1],求不等式f(x)<0的解集.
(1)若f(x)为偶函数,求实数a的值;
(2)若a∈[-1,1],求不等式f(x)<0的解集.
考点:函数恒成立问题,二次函数的性质
专题:转化思想,函数的性质及应用
分析:(1)利用函数f(x)为偶函数,得到方程即可求实数a的值;
(2)若a∈[-1,1],转化不等式f(x)<0为g(a)<0,推出不等式求解即可得到x的解集.
(2)若a∈[-1,1],转化不等式f(x)<0为g(a)<0,推出不等式求解即可得到x的解集.
解答:
解:(1)函数f(x)=ax2-(a+1)x+1.是偶函数,
∴a+1=0,解得a=-1.
(2)∵ax2-(a+1)x+1=a(x2-x)+(1-x),
令g(a)=a(x2-x)+(1-x),当x2-x=0时,x=0或x=1,不等式f(x)<0无解.
则g(a)是关于a的一次函数,
g(a)为[-1,1]上g(a)<0,
可得:
,
解得x∈∅,
综上,x的取值范围是∅.
∴a+1=0,解得a=-1.
(2)∵ax2-(a+1)x+1=a(x2-x)+(1-x),
令g(a)=a(x2-x)+(1-x),当x2-x=0时,x=0或x=1,不等式f(x)<0无解.
则g(a)是关于a的一次函数,
g(a)为[-1,1]上g(a)<0,
可得:
|
解得x∈∅,
综上,x的取值范围是∅.
点评:本题主要考查了一元二次不等式的解法,以及不等式恒成立问题,综合性较强,考查学生的转化能力.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
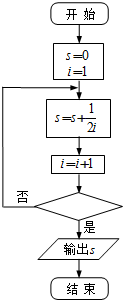 如图给出的是计算
如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
| A、i>8? | B、i>9? |
| C、i>10? | D、i>11? |