题目内容
20.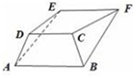 我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )
我国古代数学名著《九章算术》中有:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?”羡除即三个面是等腰梯形、两侧面是三角形的五面梯形ABCDEF隧道(如图),其中,等腰梯形ABCD的下、上底边长分别为6尺和1丈,高为3尺,平面ABCD⊥平面ABFE,等腰梯形ABFE的上底边长为8尺,高为7尺,则得到此“羡除”的容积( )| A. | 约84立方尺 | B. | 约为105立方尺 | C. | 恰为84立方尺 | D. | 恰为105立方尺 |
分析 五面体EF-ABCD中,四边形ADEF,ABCD,EFBC均为等腰梯形,EF∥AD∥BC,△ABF,△CDE均为直角三角形,连接BE,BD,AE,得到三个三棱锥,设三棱锥BAEF的体积为V1,三棱锥BAED的体积为V2,三棱锥BDEC的体积为V3,由此能求出五面体的体积.
解答 解:本题是求规则形状的五面体的体积,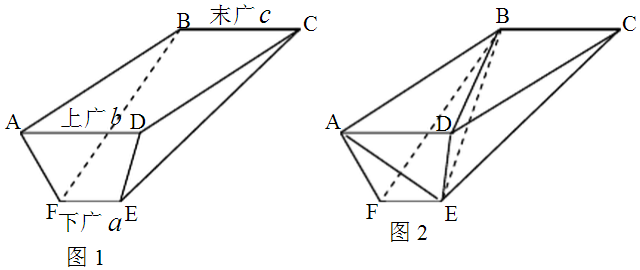
如图,五面体EF-ABCD中,四边形ADEF,ABCD,EFBC均为等腰梯形,
EF∥AD∥BC,△ABF,△CDE均为直角三角形,
AB⊥AF,CD⊥DE,设下广EF=a,上广AD=b,末广BC=c,
高EF到平面ABCD的距离为h,AD与BC的距离为l,
连接BE,BD,AE,如图2,
得到三个三棱锥,设三棱锥BAEF的体积为V1,三棱锥BAED的体积为V2,三棱锥BDEC的体积为V3,
则${V}_{3}=\frac{1}{6}clh$,${V}_{2}=\frac{1}{6}blh$,$\frac{{V}_{1}}{{V}_{2}}$=$\frac{b}{a}$,${V}_{1}=\frac{a}{b}{V}_{2}$,
∴${V}_{1}=\frac{a}{b}{{V}_{2}}^{\;}$=$\frac{1}{6}alh$,
∴五面体的体积:
V=V1+V2+V3=$\frac{1}{6}$(a+b+c)×h×l=$\frac{1}{6}$(6+10+8)×3×7=84(立方尺).
故选:C.
点评 本题考查几何体的体积及直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查考查推理论证能力、运算求解能力、空间想象能力,考查化归转化思想,数形结合思想,是中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
10.“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有X人,超过10000步的有Y人,设ξ=|X-Y|,求ξ的分布列及数学期望.
| 步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
| 男 | 1 | 2 | 3 | 6 | 8 |
| 女 | 0 | 2 | 10 | 6 | 2 |
| 积极型 | 懈怠型 | 总计 | |
| 男 | 14 | 8 | 22 |
| 女 | 6 | 12 | 18 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
8.已知$\overrightarrow{a}$为单位向量,$\overrightarrow{b}$=(0,2),且$\overrightarrow{a}$$•\overrightarrow{b}$=1,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
12.某单位共有10名员工,他们某年的收入如表:
(1)求该单位员工当年年薪的平均值和中位数;
(2)从该单位中任取2人,此2人中年薪收入高于7万的人数记为ξ,求ξ的分布列和期望;
(3)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元,5.5万元,6万元,8.5万元,预测该员工第五年的年薪为多少?
附:线性回归方程$\widehaty=\widehatbx+\widehata$中系数计算公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{7}{5}=1.4$,$\widehata=\overline y-\widehatb\overline x$,其中$\overline x,\overline y$为样本均值.
| 员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(2)从该单位中任取2人,此2人中年薪收入高于7万的人数记为ξ,求ξ的分布列和期望;
(3)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元,5.5万元,6万元,8.5万元,预测该员工第五年的年薪为多少?
附:线性回归方程$\widehaty=\widehatbx+\widehata$中系数计算公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{7}{5}=1.4$,$\widehata=\overline y-\widehatb\overline x$,其中$\overline x,\overline y$为样本均值.
9.已知函数f(x)=x2+bx+c在x=-1处取得极值-1,那么f(x)=( )
| A. | x2-2x-4 | B. | x2+x-1 | C. | x2+2x | D. | x2-2 |
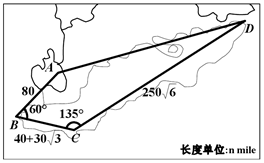 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$. 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.