题目内容
袋中有大小、形状相同的黑、白球各一个,现在有放回地随机摸取3次,每次摸一个球,若摸到黑球得1分,摸到白球得2分,则3次摸球所得总分超过4分的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:本题是一个古典概型,试验发生包含的事件数是8,则满足条件的事件可以通过列举得到共有4个,根据古典概型的概率公式得到结果
解答:
解:一共有8种不同的结果,列举如下:
(黑、黑、黑)、(黑、黑、白)、(黑、白、黑)、(黑、白、白)、(白、黑、黑)、(白、黑、白)、(白、白、黑)、(白、白、白)
记“3次摸球所得总分超过4分”为事件A,
则事件A包含的基本事件为:(黑、白、白)、(白、白、黑)、(白、白、白))(白、黑、白)
即A包含的基本事件数为4,基本事件总数为8,
所以事件A的概率为P(A)=
故选A
(黑、黑、黑)、(黑、黑、白)、(黑、白、黑)、(黑、白、白)、(白、黑、黑)、(白、黑、白)、(白、白、黑)、(白、白、白)
记“3次摸球所得总分超过4分”为事件A,
则事件A包含的基本事件为:(黑、白、白)、(白、白、黑)、(白、白、白))(白、黑、白)
即A包含的基本事件数为4,基本事件总数为8,
所以事件A的概率为P(A)=
| 1 |
| 2 |
故选A
点评:本题考查用列举法列举出所有的事件数,考查古典概型的概率公式,考查列举思想应用时要注意做到不重不漏,本题好似一个基础题.

练习册系列答案
相关题目
如图,设全集U=N,集合A={1,3,5,7,8},B={1,2,3,4,5},则图中阴影部分表示的集合为( 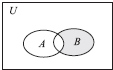

| A、{2,4} |
| B、{7,8} |
| C、{1,3,5} |
| D、{1,2,3,4,5} |
曲线y=xe2x-1在点(1,e)处切线的斜率等于( )
| A、2e | B、e | C、3e | D、1 |
若f′(x0)=A,则
等于( )
| lim |
| △x→0 |
| f(x0-△x)-f(x0) |
| △x |
| A、A | ||
| B、-A | ||
C、
| ||
| D、以上都不是 |
已知向量
,
满足|
|=2,|
|=
,且(
+
)•
=6,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题正确的是( )
| A、异面直线a,b不垂直,则不存在互相垂直的平面α,β分别过a,b |
| B、直线l不垂直平面α,则α内不存在与l垂直的直线 |
| C、直线l与平面α平行,则过α内一点有且只有一条直线与l平行 |
| D、平面α,β垂直,则过α内一点有无数条直线与β垂直 |