题目内容
已知
=(1,0),
=(-1,
),
=(cosα,sinα),则
与
的夹角的取值范围是 .
| OA |
| OC |
| 3 |
| CB |
| OA |
| OB |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
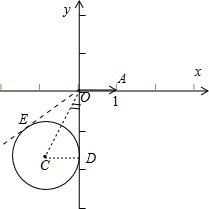
分析:由题知点B在以C(-1,
)为圆心,1为半径的圆上,所以本题应采用数形结合来解题,由图来分析其夹角的最大值点、最小值点,从而得出结论.
| 3 |
解答:
 解:∵
解:∵
=(1,0),
=
+
=(-1,
)+(cosα,sinα)=(cosα-1,sinα+
),
令x=cosα-1,y=sinα+
,则有 (x+1)2+(y-
)2=1,
故点B在以C(-1,
)为圆心、半径等于1的圆上,如图:
直角三角形OCD中,sin∠COD=
=
,∴∠COD=
=∠COE.
故
与
的夹角的最小值为∠AOD=
,最大值为∠AOE=
+
+
=
,
即
与
的夹角的取值范围是[
,
],
故答案为:[
,
].
 解:∵
解:∵| OA |
| OB |
| OC |
| CB |
| 3 |
| 3 |
令x=cosα-1,y=sinα+
| 3 |
| 3 |
故点B在以C(-1,
| 3 |
直角三角形OCD中,sin∠COD=
| OD |
| OC |
| 1 |
| 2 |
| π |
| 6 |
故
| OA |
| OB |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
即
| OA |
| OB |
| π |
| 2 |
| 5π |
| 6 |
故答案为:[
| π |
| 2 |
| 5π |
| 6 |
点评:本题考查向量的坐标运算及向量的数量积与夹角,解题的关键是求出点B的轨迹,结合圆的性质进行求解,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从半径R的球内接正方体的8个顶点及球心这9个点中任取2个点,则这两个点间的距离小于或等于半径的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合A=[0,1),B=[1,2],函数f(x)=
,x0∈A,且f[f(x0)]∈A,则x0 的取值范围是( )
|
A、(
| ||
B、[0,
| ||
C、(log2
| ||
| D、(log32,1) |
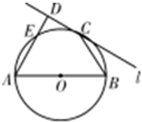 如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为