题目内容
5．若实数x，y，满足2x-y-5=0，则$\sqrt{{x^2}+{y^2}}$的最小值是（ ）| A． | $\frac{{\sqrt{5}}}{5}$ | B． | 1 | C． | $\sqrt{5}$ | D． | 5 |
分析 $\sqrt{{x^2}+{y^2}}$的几何意义是原点到直线2x-y-5=0上的点的距离，运用点到直线的距离公式计算即可得到所求值．
解答 解：$\sqrt{{x^2}+{y^2}}$的几何意义是原点到直线2x-y-5=0上的点的距离，
由点到直线的距离公式可得最小值为d=$\frac{|0-0-5|}{\sqrt{4+1}}$=$\sqrt{5}$．
故选：C．
点评 本题考查函数的最值的求法，注意运用几何意义，以及点到直线的距离公式，考查运算能力，属于基础题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
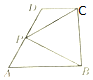如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），P为线段AD（含端点）上一个动点，设$\overrightarrow{AP}=x\overrightarrow{AD}，\overrightarrow{PB}•\overrightarrow{PC}=y$，对于函数y=f（x），给出以下三个结论：①当a=2时，函数f（x）的值域为[1，4]；②对于任意的a＞0，均有f（1）=1；③对于任意的a＞0，函数f（x）的最大值均为4．其中所有正确的结论序号为②③．
10．设f（x）为定义在R上的奇函数，当x≥0时，f（x）=2x+m（m为常数），则f（-1）=（ ）
| A． | 3 | B． | 1 | C． | -1 | D． | -3 |
17．设双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左、右焦点分别为F1，F2，过F2的直线与双曲线的右支交于两点A，B，若|AF1|：|AB|=3：4，且F2是AB的一个四等分点，则双曲线C的离心率是（ ）
| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\frac{{\sqrt{10}}}{2}$ | C． | $\frac{5}{2}$ | D． | 5 |