题目内容
【题目】已知函数![]() (其中
(其中![]() 是常数,
是常数,![]() ,
,![]() ),函数
),函数![]() 的导函数为
的导函数为![]() ,且
,且![]() .
.
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,试求
,试求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
, ![]() .
.
【解析】
试题分析:(Ⅰ)若![]() ,则
,则![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,再求得
,再求得![]() ,
,![]() 的值,即可求得曲线
的值,即可求得曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求出导数,再由![]() ,求得
,求得![]() ,令
,令 ![]() ,得
,得![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,接下来分类讨论
,接下来分类讨论![]() 与1的大小,求得函数
与1的大小,求得函数![]() 的单调区间,求得最大值,解方程即可得
的单调区间,求得最大值,解方程即可得![]() ,
,![]() 的值.
的值.
试题解析:(Ⅰ)若![]() ,则
,则![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,
,![]()
所以![]() ,
,![]()
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
即![]() .
.
(Ⅱ)由![]()
得![]()
因为![]() ,所以
,所以![]() 求得
求得![]()
所以![]() ,
,
![]()
令![]() ,得
,得![]() ,
,![]()
因为![]() ,所以
,所以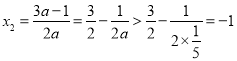
令![]() ,得
,得![]()
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]()
由![]() ,
,![]()
所以![]()
所以方程![]() 无解
无解
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增
上单调递增
所以![]() ,即
,即![]()
解得![]()
由![]() ,得
,得![]()

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者.

(1)从服药的50名患者中随机选出一人,求此人指标x的值小于1.7的概率;
(2)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
(3)若指标x小于1.7且指标y大于60就说总生理指标正常(例如图中B、D两名患者的总生理指标正常),根据上图,完成下面![]() 列联表,并判断能否有95%的把握认为总生理指标正常与是否服药有关,说明理由;
列联表,并判断能否有95%的把握认为总生理指标正常与是否服药有关,说明理由;
总生理指标正常 | 总生理指标不正常 | 总计 | |
服药 | |||
不服药 | |||
总计 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:
![]()