题目内容
4. 如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点.
如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点.(1)求证:AF⊥面EDP;
(2)设异面直线EM与AF所成的角为θ,求cosθ的最大值.
分析 (1)首先以AB,AD,AQ三直线为x,y,z轴,建立空间直角坐标系,并设正方形边长为2,证明$\overrightarrow{AF}$•$\overrightarrow{ED}$=0,$\overrightarrow{AF}$•$\overrightarrow{DP}$=0,即可证明AF⊥面EDP;
(2)M(0,y,2),从而可求出$\overrightarrow{EM}$=(-1,y,2),$\overrightarrow{AF}$=(2,1,0),由cosθ=|cos<$\overrightarrow{EM}$,$\overrightarrow{AF}$>|=$\frac{2-y}{\sqrt{{y}^{2}+5}•\sqrt{5}}$,对函数f(y)=$\frac{2-y}{\sqrt{{y}^{2}+5}•\sqrt{5}}$求导,根据导数符号即可判断该函数为减函数,从而求出cosθ的最大值.
解答  (1)证明:根据已知条件,AB,AD,AQ三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,设AB=2,则:
(1)证明:根据已知条件,AB,AD,AQ三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,设AB=2,则:
A(0,0,0),E(1,0,0),F(2,1,0),D(0,2,0),P(0,2,2)
∴$\overrightarrow{AF}$=(2,1,0),$\overrightarrow{ED}$=(-1,2,0),$\overrightarrow{DP}$=(0,0,2),
∴$\overrightarrow{AF}$•$\overrightarrow{ED}$=0,$\overrightarrow{AF}$•$\overrightarrow{DP}$=0,
∴AF⊥ED,AF⊥DP,
∵ED∩DP=D,
∴AF⊥面EDP;
(2)解:M在线段PQ上,设M(0,y,2),0≤y≤2;
∴$\overrightarrow{EM}$=(-1,y,2),$\overrightarrow{AF}$=(2,1,0),
∴cosθ=|cos<$\overrightarrow{EM}$,$\overrightarrow{AF}$>|=$\frac{2-y}{\sqrt{{y}^{2}+5}•\sqrt{5}}$;
设f(y)=$\frac{2-y}{\sqrt{{y}^{2}+5}•\sqrt{5}}$,f′(y)=$\frac{-2y-5}{\sqrt{5}({y}^{2}+5)\sqrt{{y}^{2}+5}}$
函数g(y)=-2y-5是一次函数,且为减函数,g(0)=-5<0;
∴g(y)<0在[0,2]恒成立,∴f′(y)<0;
∴f(y)在[0,2]上单调递减;
∴y=0时,f(y)取到最大值$\frac{2}{5}$.
点评 考查建立空间直角坐标系,利用空间向量解决异面直线所成角的问题,异面直线所成角的概念及其范围,向量夹角的概念及其范围,以及向量夹角余弦的坐标公式,函数导数符号和函数单调性的关系.

 名校课堂系列答案
名校课堂系列答案| A. | lg$\frac{2}{5}$ | B. | 1 | C. | -1 | D. | lg$\frac{5}{2}$ |
| A. | 若x≥3,则x2>9 | B. | 若x2≤9,则x<3 | C. | 若x2>9,则x≥3 | D. | 若x2≥9,则x>3 |
| A. | 252 盏 | B. | 256盏 | C. | 508 盏 | D. | 512盏 |

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | -$\frac{1}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
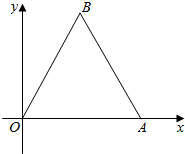 正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.
正△AOB的边长为a,建立如图所示的直角坐标系xOy,则它的直观图的面积是$\frac{\sqrt{6}{a}^{2}}{16}$.