题目内容

20．设a=sin17°cos45°+cos17°sin45°，b=2cos213°，c=$\frac{\sqrt{3}}{2}$，则有（　　）
A．a＜b＜cB．b＜c＜aC．c＜a＜bD．b＜a＜c

分析 利用两角和的正弦公式、诱导公式化简a、b的寒暑假解析式，再利用正弦函数的单调性，得出结论．

解答 解：∵a=sin17°cos45°+cos17°sin45°=sin（17°+45°）=sin62°，
b=2cos213°=2cos213°-1+1=cos26°+1=sin63°+1，c=$\frac{\sqrt{3}}{2}$=sin60°，
而函数y=sinx在（ 0°，90°）上单调递增，∴b＞a＞c，
故选：C．

点评 本题主要考查两角和的正弦公式、诱导公式，正弦函数的单调性，属于基础题．

练习册系列答案
相关题目
10．已知直线l的参数方程$\left\{\begin{array}{l}{x=t}\\{y=1+2t}\end{array}\right.$（t为参数），若以原点O为极点，x轴的正半轴为极轴，建立极坐标系，圆C的极坐标方程为ρ=2$\sqrt{2}$sin（θ+$\frac{π}{4}$）．则圆的直角坐标方程为（x-1）2+（y-1）2=2，直线l和圆C的位置关系为相交（填相交、相切、相离）．
11．如图，在三棱柱ABC-A1B1C1中，面ABB1A1为矩形，AB=1，AA1=$\sqrt{2}$，D为AA1的中点，BD与AB1交于点O，CO⊥面ABB1A1
（Ⅰ）证明：BC⊥AB1
（Ⅱ）若OC=OA，求二面角A-BC-B1的余弦值．
8．已知函数y=x2的图象在点（x0，x02）处的切线为直线l，若直线l与函数y=lnx（x∈（0，1））的图象相切，则满足（　　）
A．x0∈（$\sqrt{2}$，$\sqrt{3}$）B．x0∈（1，$\sqrt{2}$）C．x0∈（0，$\frac{1}{2}$）D．x0∈（$\frac{1}{2}$，1）
15．已知函数f（x）=x4-2x3，g（x）=-4x2+4x-2，x∈R．
（1）求f（x）的最小值；
（2）证明：f（x）＞g（x）．
5．不等式$\left\{\begin{array}{l}y≤2x\\ y-\frac{1}{2}x≥0\\ x+y≤k\end{array}\right.$表示的区域面积大于或等于$\frac{3}{2}$，则实数k的取值范围是（　　）
A．k≥1B．k≥2C．k≥3D．k≥4
12．已知正项等差数列{an}的前n项和为Sn，且满足${a_1}+{a_5}=\frac{1}{3}a_3^2，{S_7}=56$．
（1）求数列{an}的通项公式；
（2）求数列$\left\{{{3^{a_n}}}\right\}$的前n项和．
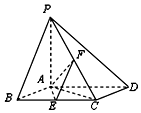9．如图所示，已知四棱锥P-ABCD中，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是线段BC，PC的中点
（1）证明：AE⊥PD
（2）若H为PD上的动点，EH与平面PAD所成最大角的正切值为$\sqrt{3}$，求二面角E-AF-C的余弦值．
10．已知p：-1＜x＜0，q：m-1＜x＜m+1，若p是q的充分条件，则m的取值范围是[-1，0]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网