题目内容
8.已知实数x,y满足|2x+y-2|≥|6-x-3y|且|x|≤4,则|3x-4y|的最大值为32.分析 根据条件画出(x,y)的范围,求出可行域内的点到直线3x-4y=0的距离的最大值,可得|3x-4y|的最大值.
解答 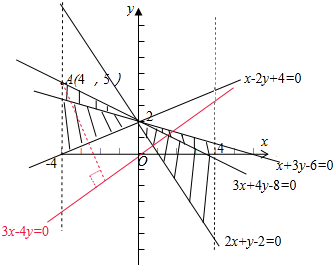 解:实数x,y满足|2x+y-2|≥|6-x-3y|,
解:实数x,y满足|2x+y-2|≥|6-x-3y|,
即|2x+y-2|≥|x+3y-6|,且|x|≤4,
∴$\left\{\begin{array}{l}{2x+y-2≥0}\\{x+3y-6≥0}\\{x-2y+4≥0}\\{-4≤x≤4}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{2x+y-2≤0}\\{x+3y-6≤0}\\{x-2y+4≤0}\\{-4≤x≤4}\end{array}\right.$ ②,
或$\left\{\begin{array}{l}{2x+y-2≥0}\\{x+3y-6≤0}\\{3x+4y-8≥0}\\{-4≤x≤4}\end{array}\right.$ ③,或$\left\{\begin{array}{l}{2x+y-2≤0}\\{x+3y-6≥0}\\{3x+4y-8≤0}\\{-4≤x≤4}\end{array}\right.$ ④.
由①②③④可得点(x,y)的可行域如图
(阴影部分):
由于可行域内的点A(-4,5)到直线3x-4y=0
的距离的最大值为$\frac{|3×(-4)-4×5|}{5}$=$\frac{32}{5}$,
故|3x-4y|的最大值为32,
故答案为:32.
点评 本题主要考查绝对值不等式的解法,简单的线性规划,点到直线的距离公式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.设集合A={x|$\frac{1}{2}$<x<3},B={x|(x+1)(x-2)<0},则A∩B=( )
| A. | {x|$\frac{1}{2}$<x<2} | B. | {x|-1<x<3} | C. | {x|$\frac{1}{2}$<x<1} | D. | {x|1<x<2} |