题目内容
12.求经过直线l1:3x-4y-1=0与直线l2:x+2y+8=0的交点M,且满足下列条件的直线l的方程:(1)与直线2x+y+5=0平行;
(2)与直线2x+y+5=0垂直.
分析 联立$\left\{\begin{array}{l}{3x-4y-1=0}\\{x+2y+8=0}\end{array}\right.$,解得交点M,
(1)由平行关系可得直线的斜率,进而可得点斜式方程,化为一般式即可;
(2)由垂直关系可得直线的斜率,进而可得点斜式方程,化为一般式即可.
解答 解:联立$\left\{\begin{array}{l}{3x-4y-1=0}\\{x+2y+8=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-3}\\{y=-\frac{5}{2}}\end{array}\right.$,可得交点M(-3,-$\frac{5}{2}$).
(1)若直线平行于直线2x+y+5=0,则斜率为-2,
故可得方程为$y+\frac{5}{2}=-2(x+3)$,即4x+2y+17=0;
(2)若直线垂直于直线2x+y+5=0,则斜率为$\frac{1}{2}$,
故可得方程为$y+\frac{5}{2}=\frac{1}{2}(x+3)$,即x-2y-2=0.
点评 本题考查了直线的交点、相互平行垂直的直线与斜率之间的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
2.利用独立性检测来考查两个分类变量X,Y是否有关系,当随机变量K2的值( )
| A. | 越大,“X与Y有关系”成立的可能性越大 | |
| B. | 越大,“X与Y有关系”成立的可能性越小 | |
| C. | 越小,“X与Y有关系”成立的可能性越大 | |
| D. | 与“X与Y有关系”成立的可能性无关 |
17.某单位拟安排6位员工在今年5月28日至30日(端午节假期)值班,每天安排2人,每人值班1天.若6位员工中的甲不值28日,乙不值30日,则不同的安排方法共有( )
| A. | 30种 | B. | 36种 | C. | 42种 | D. | 48种 |
1.已知复数z=$\frac{4-3i}{6+8i}$(i是虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{7}{48}$ | D. | $\frac{3}{10}$ |
6.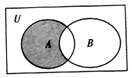 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )| A. | ∁U(A∩B) | B. | ∁U(A∪B) | C. | A∩(∁UB) | D. | (∁UA)∩B |