题目内容

1．已知数列{an}是等差数列，且a7-2a4=6，a3=2，则公差d=（　　）
A．2$\sqrt{2}$B．4C．8D．16

分析 利用等差数列的通项公式即可得出．

解答 解：∵数列{an}是等差数列，且a7-2a4=6，a3=2，
∴$\left\{\begin{array}{l}{{a}_{1}+6d-2（{a}_{1}+3d）=6}\\{{a}_{1}+2d=2}\end{array}\right.$，解得a1=-6，d=4．
则公差d=4．
故选：B．

点评 本题考查了等差数列的通项公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
9．设tanα=1，3sinβ=sin（2α+β），求tan（2α+2β）．
12．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow a$|=1，$|2\overrightarrow a-\overrightarrow b|$=$2\sqrt{3}$，$\overrightarrow a$在$\overrightarrow b$方向的投影为$\frac{1}{2}$，则$\overrightarrow b•（\overrightarrow a+2\overrightarrow b）$=34．
9．如图所示的程序框图，当a1=1，k=2016时，输出的结果为$\frac{2016}{2017}$．
16．执行如图所示的程序框图，如果输入的t=50，则输出的n=（　　）
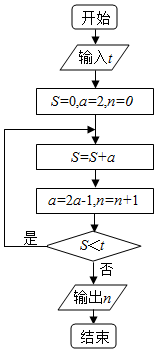
A．5B．6C．7D．8
6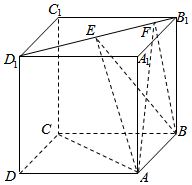．如图，正方体ABCD-A1B1C1D1的棱长为1，E，F是线段B1D1上的两个动点，且EF=$\frac{\sqrt{2}}{2}$，则下列结论中错误的是（　　）
A．AC⊥BFB．三棱锥A-BEF的体积为定值
C．EF∥平面ABCDD．面直线AE、BF所成的角为定值
13．已知△ABC的内角A，B，C的对边分别为a，b，c，$\overrightarrow{m}$=（$\frac{a}{sin（A+B）}$，c-2b），$\overrightarrow{n}$=（sin2C，1），且满足$\overrightarrow{m}•\overrightarrow{n}$=0．
（1）求∠A的大小；
（2）若a=1，求△ABC周长的取值范围．
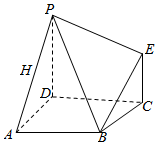10．如图，多面体ABCDPE的底面ABCD是平行四边形，AD=AB=2，$\overrightarrow{AB}$$•\overrightarrow{AD}$=0，PD⊥平面ABCD，EC∥PD，且PD=2EC=2．
（1）若棱AP的中点为H，证明：HE∥平面ABCD；
（2）求二面角A-PB-E的大小．
11．函数$f（x）=\frac{1}{x}+a$的反函数的图象经过点（2，1），则实数a=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网