题目内容
19.用五点法画出y=$\frac{1}{2}$sin(2x-$\frac{π}{3}$)在一个周期内的图象.分析 直接根据五点法画图的步骤和方法进行作图即可.
解答 解:列表如下:
| 2x-$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ | $\frac{7π}{6}$ |
| y=$\frac{1}{2}$sin(2x-$\frac{π}{3}$) | 0 | $\frac{1}{2}$ | 0 | -$\frac{1}{2}$ | 0 |
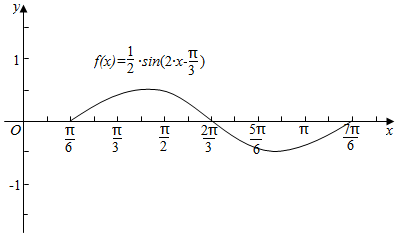
点评 本题重点考查了五点法作函数y=Asin(ωx+φ)的图象,三角函数的图象与性质,属于基础题.

练习册系列答案
相关题目
14.“$\frac{|C|}{\sqrt{A^2+B^2}}$≤a”是“曲线Ax+By+C=0与$\frac{x^2}{a}$+$\frac{y^2}{b}$=1(a>b>0)有公共点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.已知定义在[3m-1,m]的函数f(x)=-mx2+(n+1)x,且f(x-2)是偶函数,则(n-m)2=( )
| A. | 0 | B. | $\frac{25}{16}$ | C. | $\frac{121}{16}$ | D. | 16 |
11.设偶函数f(x)在[0,+∞)上为增函数,则不等式f(x)>f(2x十1)的解集为( )
| A. | ∅ | B. | {x|x<-1或x>$\frac{1}{3}$} | C. | {x|x>1或x<$\frac{1}{3}$} | D. | {x|-1<x<-$\frac{1}{3}$} |