题目内容
已知函数f(x)<0定义在R上的奇函数,当x>0时,f(x)=xlnx,给出下列命题中正确命题个数是:( )
①当x<0时,f(x)=xln(-x)
②函数f(x)有2个零点
③f(x)>0的解集为(-1,0)∪(1,+∞)
④?x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤
.
①当x<0时,f(x)=xln(-x)
②函数f(x)有2个零点
③f(x)>0的解集为(-1,0)∪(1,+∞)
④?x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤
| 2 |
| e |
| A、1 | B、2 | C、3 | D、4 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据奇函数的性质,f(-x)=-f(x),加以判断.
解答:
解:函数的图象如图:
x<0,则-x>0,
∴f(-x)=-xln(-x)
∵函数是奇函数,
∴f(x)=-f(x)=xln(-x),故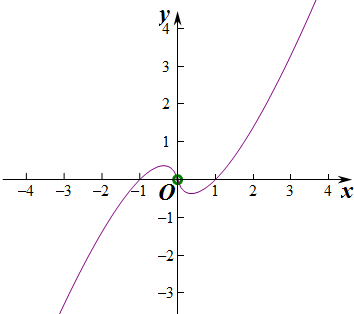 ①正确;
①正确;
∴f(0)=0,故函数的零点由三个,故②不正确;
由图象可知:③正确;
当x∈[-1,1]时,f(x)max=-
ln
=
,
f(x)min=
ln
=-
,
∴④?x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤
.故④正确.
故选C
x<0,则-x>0,
∴f(-x)=-xln(-x)
∵函数是奇函数,
∴f(x)=-f(x)=xln(-x),故
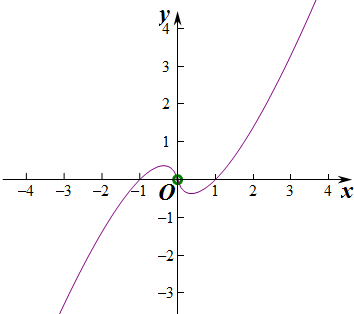 ①正确;
①正确;∴f(0)=0,故函数的零点由三个,故②不正确;
由图象可知:③正确;
当x∈[-1,1]时,f(x)max=-
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
f(x)min=
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
∴④?x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤
| 2 |
| e |
故选C
点评:本题考查了函数解析式的求法,零点的求法,以及函数的单调性,属于基础题目.利用绘画函数图象,通过图象得到结论.

练习册系列答案
相关题目
函数f(x)=x-lg
-2的零点所在区间为( )
| 1 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
已知∠AOB=60°,在∠AOB内随机作一条射线OC,则∠AOC小于15°的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题p:“a<-
“是“函数f(x)=log3(x-a)+1的图象经过第二象限”的充分不必要条件,命题q:a,b是任意实数,若a>b,则
<
.则( )
| 1 |
| 2 |
| 1 |
| a+1 |
| 1 |
| b+1 |
| A、“p且q”为真 |
| B、“p或q”为真 |
| C、p假q真 |
| D、p,q均为假命题 |
| ∫ |
-π |
| A、0 | B、1 | C、2 | D、3 |
下列函数中是奇函数,且在区间(0,+∞)上单调递增的是( )
| A、y=2x |
| B、y=-x2 |
| C、y=x3 |
| D、y=-3x |
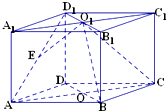 如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC与BD交于点O,A1C1与B1D1交于点O1,E为AD1的中点.
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC与BD交于点O,A1C1与B1D1交于点O1,E为AD1的中点.