题目内容
设曲线C的参数方程为
(θ是参数,a>0),直线l的极坐标方程为3ρcosθ+4ρsinθ=5,若曲线C与直线l只有一个公共点,则实数a的值是 .
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:曲线C的参数方程为
(θ是参数,a>0),利用sin2θ+cos2θ=1化为(x-a)2+(y-1)2=16.直线l的极坐标方程为3ρcosθ+4ρsinθ=5,利用
化为3x+4y-5=0.由于曲线C与直线l只有一个公共点,可得直线与圆相切,因此圆心到直线l的距离d=r,a>0,解出即可.
|
|
解答:
解:曲线C的参数方程为
(θ是参数,a>0),化为(x-a)2+(y-1)2=16.
直线l的极坐标方程为3ρcosθ+4ρsinθ=5,化为3x+4y-5=0.
∵曲线C与直线l只有一个公共点,
∴直线与圆相切,
∴圆心到直线l的距离d=
=r=4,a>0,
解得a=7.
故答案为:7.
|
直线l的极坐标方程为3ρcosθ+4ρsinθ=5,化为3x+4y-5=0.
∵曲线C与直线l只有一个公共点,
∴直线与圆相切,
∴圆心到直线l的距离d=
| |3a+4-5| | ||
|
解得a=7.
故答案为:7.
点评:本题考查了把参数方程化为普通方程、极坐标方程化为直角坐标方程、直线与圆的位置关系、点到直线的距离公式,考查了计算能力,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
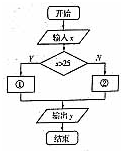 某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )
某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )| A、y=0.8xy=0.5x |
| B、y=0.5xy=0.8x |
| C、y=0.8x-7.5y=0.5x |
| D、y=0.8x+12.5y=0.8x |
一个几何体的三视图如图所示,该集合体的体积是( )


| A、30 | B、40 | C、50 | D、60 |
某程序框图如图所示,执行该程序后输出的S的值是( )
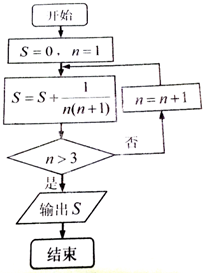

A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题p:?x∈R,x2-2x-3>0,命题q:?x0∈R,sinx0+cosx0=
,则下列判断正确的是( )
| 2 |
| A、p为真命题 |
| B、p∧q为真命题 |
| C、p∨q为假命题 |
| D、¬q为假命题 |