题目内容
20.在平面直角坐标系xOy中,已知圆C:(x-2)2+(y+1)2=5,过点P(5,0)且斜率为k的直线l与圆C相交于不同的两点A,B.(Ⅰ)求k的取值范围;
(Ⅱ)若弦长|AB|=4,求直线l的方程.
分析 (Ⅰ)直线l与圆C相交于不同的两点A,B,故圆心到直线l的距离$d=\frac{{|{2k+1-5k}|}}{{\sqrt{{k^2}+1}}}=\frac{{|{1-3k}|}}{{\sqrt{{k^2}+1}}}<\sqrt{5}$,即可求k的取值范围;
(Ⅱ)若弦长|AB|=4,利用勾股定理,求出k,即可求直线l的方程.
解答 解:(Ⅰ)由已知圆C:(x-2)2+(y+1)2=5,知圆心C(2,-1),半径$\sqrt{5}$,----(1分)
设过点P(5,0)且斜率为k的直线l:y=k(x-5),-----------------------------------(2分)
因为直线l与圆C相交于不同的两点A,B,
故圆心到直线l的距离$d=\frac{{|{2k+1-5k}|}}{{\sqrt{{k^2}+1}}}=\frac{{|{1-3k}|}}{{\sqrt{{k^2}+1}}}<\sqrt{5}$---------(5分)
得(2k+1)(k-2)<0,所以,$-\frac{1}{2}<k<2$------------------------------(7分)
(Ⅱ)弦长|AB|=4,得:$5-{(\frac{{|{1-3k}|}}{{\sqrt{{k^2}+1}}})^2}=4$----------------------------------------(8分)
解得:k=0或$k=\frac{3}{4}$y=0或是3x-4y-15=0(10分)
点评 本题考查直线方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
10.已知双曲线$E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右焦点分别为F1,F2,若E上存在点P使△F1F2P为等腰三角形,且其顶角为$\frac{2π}{3}$,则$\frac{a^2}{b^2}$的值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
8.已知x>3,则$x+\frac{4}{x-3}$的最小值为( )
| A. | 2 | B. | 4 | C. | 5 | D. | 7 |
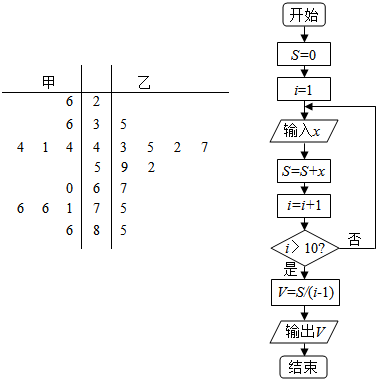 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.