题目内容
4.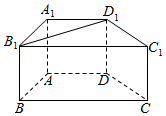 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB=AD=AA1=2.底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,∠BCD=45°.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB=AD=AA1=2.底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,∠BCD=45°.(])求三棱锥C-B1C1D1的体积;
(2)求证:B1D1⊥平面CDD1C1.
分析 (1)求出底面积,即可求三棱锥C-B1C1D1的体积;
(2)利用线面垂直的判定定理证明B1D1⊥平面CDD1C1.
解答 (1)解:∵AB=AD=2.底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,∠BCD=45°,
∴B1C1=4,
∵AA1⊥底面ABCD,AA1=2,
∴三棱锥C-B1C1D1的体积=$\frac{1}{3}×\frac{1}{2}×4×2×2$=$\frac{8}{3}$;
(2)证明:△B1C1D1中,B1C1=4,B1D1=D1C1=2$\sqrt{2}$,
∴B1C12=B1D12+D1C12,
∴B1D1⊥D1C1,
∵四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,
∴CC1⊥底面A1B1C1D1,
∴CC1⊥B1D1,
∵D1C1∩CC1=C1,
∴B1D1⊥平面CDD1C1.
点评 本题考查三棱锥C-B1C1D1的体积,线面垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
14.一位母亲记录了儿子3-9岁的身高,收集了好几组数据(略),由此建立的身高与年龄的回归模型为y=7.18x+73.95,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
| A. | 身高在145.75cm以上 | B. | 身高在145.75cm左右 | ||
| C. | 身高一定是145.75cm | D. | 身高在145.75cm以下 |
12.已知集合A={x∈Z||x|<4},B={x|x-1≥0},则A∩B等于( )
| A. | (1,4) | B. | [1,4) | C. | {1,2,3} | D. | {2,3,4} |