题目内容
14.已知直线l的斜率k=$\frac{2}{3}$,且与两坐标轴围成的三角形面积为3,求直线l的方程.分析 设直线l与两坐标轴的交点分别为(a,0),(0,b),可得$\frac{1}{2}$|ab|=3,$\frac{b}{a}$=$\frac{2}{3}$,联立解出即可得出.
解答 解:设直线l与两坐标轴的交点分别为(a,0),(0,b),
∴$\frac{1}{2}$|ab|=3,$\frac{b}{a}$=$\frac{2}{3}$,
联立解得:$\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$或$\left\{\begin{array}{l}{a=-3}\\{b=-2}\end{array}\right.$.
∴直线l的方程为$y=\frac{2}{3}x±2$.
点评 本题考查了直线的截距式、斜率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.定义在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{|x-3|-1,x>1}\\{lo{g}_{2}(x+1),0≤x≤1}\end{array}\right.$则函数g(x)=f(x)-m(0<m<1)的所有零点之和为( )
| A. | 1-2m | B. | 2m-1 | C. | 1-($\frac{1}{2}$)m | D. | ($\frac{1}{2}$)m-1 |
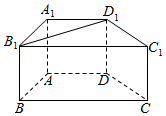 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB=AD=AA1=2.底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,∠BCD=45°.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB=AD=AA1=2.底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,∠BCD=45°.