题目内容
10．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：| 单价x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y（件） | 90 | 84 | 83 | 80 | 75 | 68 |
分析 由题意求出$\overline{x}$，$\overline{y}$，利用公式求出$\hat{a}$，即可得出线性回归方程，当x=9.5时，可得结论．
解答 解：由题意：$\overline{x}$=$\frac{1}{6}（8+8.2+8.4+8.6+8.8+9）$=8.5；
$\overline{y}$=$\frac{1}{6}（90+84+83+80+75+68）$=80．
∵$\hat{b}$=-20．
∴$\hat{a}$=80+20×8.5=250，
从而得到回归直线方程为：y=-20x+250．
当x=9.5时，可得y=60．
故答案为：60．
点评 本题考查了线性回归方程的求法及应用，属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
20．复数z=-2+i所对应的点在复平面的（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
5．命题“若a＞b，则ac＞bc”的逆否命题是（ ）
| A． | 若a＞b，则ac≤bc | B． | 若ac≤bc，则a≤b | C． | 若ac＞bc，则a＞b | D． | 若a≤b，则ac≤bc |
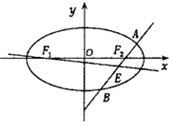已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与x轴所成的夹角为30°，且双曲线的焦距为4$\sqrt{2}$．
如图是判断“实验数”的程序框图，在[30，80]内的所有整数中，“实验数”的个数是12．