题目内容
(本小题满分13分)根据新修订的《环境空气质量标准》指出空气质量指数在 ,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
,各类人群可正常活动.某市环保局在2014年对该市进行为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
, ,
, ,
, ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.

(1)求 的值;
的值;
(2)根据样本数据,试估计这一年度的空气质量指数的平均值;
(3)用这50个样本数据来估计全年的总体数据,将频率视为概率.如果空气质量指数不超过20,就认定空气质量为“最优等级”.从这一年的监测数据中随机抽取2天的数值,其中达到“最优等级”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(1) ,(2)
,(2) ,(3)
,(3)
【解析】
试题分析:先利用频率和为1,求出 ,再利用平均值公式求出平均值,第三步从这一年的监测数据中随机
,再利用平均值公式求出平均值,第三步从这一年的监测数据中随机
抽取2天的数值,其中达到“最优等级”的天数为 ,
, 可取值为0,1,2;由于指数达到“最优等级”的
可取值为0,1,2;由于指数达到“最优等级”的
概率为0.3,则 ,利用二项分布概率公式,列出概率分布列,求出数学期望;
,利用二项分布概率公式,列出概率分布列,求出数学期望;
试题解析:(1)先求 ,根据频率分布直方图中的数据可知
,根据频率分布直方图中的数据可知 ,则
,则

 ;
;
(2)50个样本中空气质量指数的平均值为:


 ;由样本估计总体,可估计这一年度空气质量指数的平均值为25.6;
;由样本估计总体,可估计这一年度空气质量指数的平均值为25.6;
(3)利用样本估计总体,该年度空气质量指数在 内为“最优等级”,且指数达到“最优等级”的概率为0.3,则
内为“最优等级”,且指数达到“最优等级”的概率为0.3,则 ,
, 的可能取值为0,1,2;
的可能取值为0,1,2; ,
, =
=
 ,
, ;
;
 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
 (或
(或 )
)
 的数学期望为
的数学期望为 ;
;
考点: 1.概率分布直方图;2.概率分布列与数学期望;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





 B.
B. C.
C. D.
D.
 为实数,且
为实数,且 ,
, 为实数,且
为实数,且 ,则A∩B的元素个数为
,则A∩B的元素个数为 的展开式的常数项是
的展开式的常数项是 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: .
. 的直角坐标方程;
的直角坐标方程; 与圆
与圆 的位置关系.
的位置关系. 为纯虚数,若
为纯虚数,若 (
( 为虚数单位),则实数
为虚数单位),则实数 的值为 .
的值为 . ,
, 且
且 ”是“数列
”是“数列 为等比数列”的( )
为等比数列”的( ) ,
, ,若对于任一实数
,若对于任一实数 ,
, 与
与 至少有一个为正数,则实数
至少有一个为正数,则实数 的取值范围是 ( )
的取值范围是 ( )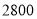 人,其中高一年级
人,其中高一年级 人,高二年级
人,高二年级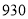 人,高三年级
人,高三年级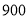 人,现采用分层抽样的方法,抽取
人,现采用分层抽样的方法,抽取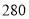 人进行体育达标检测,则抽取高二年级学生人数为 .
人进行体育达标检测,则抽取高二年级学生人数为 .