题目内容
6.函数f(x)=$\frac{1+lnx}{x}$.(Ⅰ)判断f(x)的单调性,并求f(x)的极值;
(Ⅱ)求证:当x≥1时,$\frac{(x+1)(1+lnx)}{x}$≥2.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)问题转化为$\frac{(x+1)(1+lnx)}{x}$≥x+1,求出x+1的最小值即可.
解答 解:(Ⅰ)f(x)的定义域是(0,+∞),
f′(x)=-$\frac{lnx}{{x}^{2}}$,
令f′(x)>0,解得:0<x<1,
令f′(x)<0,解得:x>1,
故f(x)在(0,1)递增,在(1,+∞)递减,
故f(x)极大值=f(1)=1;
证明:(Ⅱ)由(Ⅰ)得:x≥1时,$\frac{1+lnx}{x}$的最小值是1,
故$\frac{(x+1)(1+lnx)}{x}$≥x+1≥2,
故原不等式得证.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
7.如图描述的是我国2014年四个季度与2015年前三个季度三大产业GDP累计同比贡献率,以下结论正确的是( )


| A. | 2015年前三个季度中国GDP累计比较2014年同期增速有上升的趋势 | |
| B. | 相对于2014年,2015年前三个季度第三产业对GDP的贡献率明显增加 | |
| C. | 相对于2014年,2015年前三个季度第二产业对GDP的贡献率明显增加 | |
| D. | 相对于2014年,2015年前三个季度第一产业对GDP的贡献率明显增加 |
17.执行如图所示的程序框图,输出S的值为( )
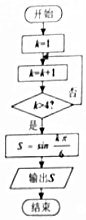

| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
14.已知输入的x=11,执行如图所示的程序框图,则输出的x的值为( )


| A. | 23 | B. | 47 | C. | 95 | D. | 191 |
1.已知全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则(∁UM)∪(∁UN)=( )
| A. | {2,4} | B. | {2,3,5} | C. | {1,3,4,5} | D. | {2,3,4,5} |
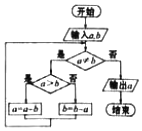 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为98,63,则输出的a为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为98,63,则输出的a为( )