题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，且满足csin A＝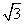
acos C.
(1)求角C的大小；
(2)求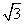sin A－sin
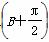的最大值，并求取得最大值时角A，B的大小．
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，且满足csin A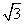＝acos C.
(1)求角C的大小；
(2)求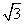sin A－sin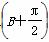的最大值，并求取得最大值时角A，B的大小．
名校课堂系列答案
cos2 θ＝3.
，若斜边所在直线的倾斜角为钝角，则斜边所在直线的方程为______________．
＝
＝
.
上，∠PAB＝θ，用θ的三角函数表示△PAC的面积，并求△PAC面积最大值．
内角A、B、C的对边分别为a、b、c,23cos2A＋co
s 2A＝0，a＝7，c＝6，则b＝( )
图象上各点的横坐标缩短到原来的
倍(纵坐标不变)，再将图象向右平移
个单位，那么所得图象的一条对称轴方程为( )
b＝(
sin x，cos 2x)，x∈R，设函数f(x)＝a·b.
上的最大值和最小值．
的值为 ( )
，且角α的终边经过点P(x,2)，则P点的横坐标x是( )
B．±2
D．－2