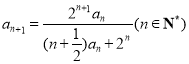题目内容
【题目】(本小题满分10分)
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?
【答案】分别生产甲、乙两种产品3吨和4吨时可获得最大利润,最大利润是27万元.
【解析】设该企业生产甲产品为![]() 吨,乙产品为
吨,乙产品为![]() 吨,
吨,
该企业可获得利润为![]() ,且
,且 ,(3分)
,(3分)
作出线性约束条件所表示的平面区域如下图中阴影部分所示,
 (5分)
(5分)
联立![]() ,解得
,解得![]() ,由图可知,最优解为
,由图可知,最优解为![]() ,(8分)
,(8分)
所以![]() 的最大值为
的最大值为![]() (万元),故在一个生产周期内该企业分别生产甲、乙两种产品3吨和4吨时可获得最大利润,最大利润是27万元.(10分)
(万元),故在一个生产周期内该企业分别生产甲、乙两种产品3吨和4吨时可获得最大利润,最大利润是27万元.(10分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(x个月)和市场占有率(y%)的几组相关对应数据:
x | 1 | 2 | 3 | 4 | 5 |
y | 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(1)根据上表中的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过0.5%(精确到月).
附:  ,
, ![]() .
.