题目内容
3.命题:若点O和点F(-2,0)分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则$\overrightarrow{OP}$•$\overrightarrow{FP}$的取值范围为[3+2$\sqrt{3}$,+∞).判断此命题的真假,若为真命题,请做出证明;若为假命题,请说明理由.
分析 先求出双曲线方程为$\frac{{x}^{2}}{{3}^{\;}}-{y}^{2}=1$,设点P(x0,y0),则${{y}_{0}}^{2}=\frac{{{x}_{0}}^{2}}{3}-1$,(x0$≥\sqrt{3}$),由此能证明$\overrightarrow{OP}$•$\overrightarrow{FP}$的取值范围为[3+2$\sqrt{3}$,+∞).
解答 解:此命题为真命题.
证明如下:
∵F(-2,0)是已知双曲线的左焦点,∴a2+1=4,解得a2=3,
∴双曲线方程为$\frac{{x}^{2}}{{3}^{\;}}-{y}^{2}=1$,
设点P(x0,y0),则有$\frac{{{x}_{0}}^{2}}{3}-{{y}_{0}}^{2}$=1,(${x}_{0}≥\sqrt{3}$),
解得${{y}_{0}}^{2}=\frac{{{x}_{0}}^{2}}{3}-1$,(x0$≥\sqrt{3}$),
∵$\overrightarrow{FP}$=(x0+2,y0),$\overrightarrow{OP}$=(x0,y0),
∴$\overrightarrow{OP}•\overrightarrow{FP}$=${x}_{0}({x}_{0}+2)+{{y}_{0}}^{2}$=x0(x0+2)+$\frac{{{x}_{0}}^{2}}{3}-1$=$\frac{4{{x}_{0}}^{2}}{3}+2{x}_{0}-1$,
这个二次函数的对称轴为${x}_{0}=-\frac{3}{4}$,
∵${x}_{0}≥\sqrt{3}$,∴当${x}_{0}=\sqrt{3}$时,$\overrightarrow{OP}•\overrightarrow{FP}$取得最小值$\frac{4}{3}×3+2\sqrt{3}-1$=3+2$\sqrt{3}$,
∴$\overrightarrow{OP}$•$\overrightarrow{FP}$的取值范围为[3+2$\sqrt{3}$,+∞).
点评 本题考查命题真假的判断与证明,是中档题,解题时要认真审题,注意双曲线的性质的合理运用.

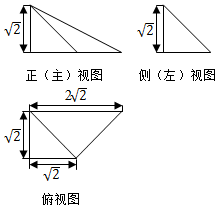
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3$\sqrt{2}$ |
| A. | ?n0∈Z,n0∉Q | B. | ?n0∉Z,n0∈Q | C. | ?n0∈Z,n0∉Q | D. | ?n0∉Z,n0∈Q |
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | ac>bc | C. | $\sqrt{a}$>$\sqrt{b}$ | D. | $\frac{a}{c}$>$\frac{b}{c}$ |