Question

14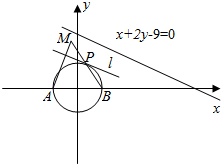．已知圆C：x²+y²=1与x轴的两个交点分别为A，B（由左到右），P为C上的动点，l过点P且与C相切，过点A作l的垂线且与直线BP交于点M，则点M到直线x+2y-9=0的距离的最大值是$2\sqrt{5}+2$．

Answer 1

分析 先利用交轨法求出M的轨迹是以（-1，0）为圆心，2为半径的圆，再利用圆心到直线的距离公式，即可得出结论．

解答 解：设P（a，b），则l的方程为ax+by=1，
∴AM的方程为bx-ay+b=0，BP的方程为bx-（a-1）y-b=0，
联立，可得M（2a-1，2b），
即x=2a-1，y=2b，
∴a=$\frac{x+1}{2}$，b=$\frac{y}{2}$，
∵a²+b²=1，
∴（x+1）²+y²=4，即M的轨迹是以（-1，0）为圆心，2为半径的圆，
圆心到直线x+2y-9=0的距离d=$\frac{|-1-9|}{\sqrt{5}}$=2$\sqrt{5}$，
∴点M到直线x+2y-9=0的距离的最大值是$2\sqrt{5}+2$．
故答案为：$2\sqrt{5}+2$．

点评 本题考查轨迹方程，考查点到直线的距离公式，考查学生分析解决问题的能力，属于中档题．