题目内容
6.已知f(x)=ax.(a>0,a≠1),若f(x)在[-2,2]的最大值为16,则a=4或$\frac{1}{4}$.分析 讨论a>1,0<a<1,运用指数函数的单调性,可得最大值,解方程可得a的值.
解答 解:当a>1时,f(x)=ax在[-2,2]递增,
即有f(2)最大,且为a2=16,解得a=4;
当0<a<1时,f(x)=ax在[-2,2]递减,
即有f(-2)最大,且为a-2=16,解得a=$\frac{1}{4}$.
综上可得a=4或$\frac{1}{4}$.
故答案为:4或$\frac{1}{4}$.
点评 本题考查函数的最值的求法,注意运用指数函数的单调性,考查运算能力,属于基础题.

练习册系列答案
相关题目
11.若函数$f(x)=\frac{x}{{({2x+1})({2x-a})}}$为奇函数,则a=( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
15.P(x,y)在线段AB上运动,已知A(2,4),B(5,-2),则$\frac{y+1}{x+1}$的取值范围是( )
| A. | [-$\frac{1}{6}$,$\frac{5}{3}$] | B. | (-∞,-$\frac{1}{6}$]∪[$\frac{5}{3}$,+∞) | C. | [-$\frac{1}{6}$,0)∁(0,$\frac{5}{3}$] | D. | (-$\frac{1}{6}$,$\frac{5}{3}$) |
16.下面是一程序,该程序的运行结果是( )


| A. | 1,2 | B. | 1,1 | C. | 2,1 | D. | 2,2 |
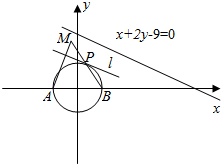 已知圆C:x2+y2=1与x轴的两个交点分别为A,B(由左到右),P为C上的动点,l过点P且与C相切,过点A作l的垂线且与直线BP交于点M,则点M到直线x+2y-9=0的距离的最大值是$2\sqrt{5}+2$.
已知圆C:x2+y2=1与x轴的两个交点分别为A,B(由左到右),P为C上的动点,l过点P且与C相切,过点A作l的垂线且与直线BP交于点M,则点M到直线x+2y-9=0的距离的最大值是$2\sqrt{5}+2$.