题目内容
3.已知函数f(x)=lnx+$\frac{a+2}{x}$,求f(x)的单调区间.分析 判断参数a+2的取值,求函数的导数,利用函数单调性和导数之间的关系进行求解即可.
解答 解:函数的定义域为(0,+∞),
若a+2=0,即a=-2时,f(x)=lnx,此时函数单调递增,递增区间为(0,+∞),
若a+2<0,即a<-2时,f(x)=lnx+$\frac{a+2}{x}$,此时函数单调递增,递增区间为(0,+∞),
若a+2>0,即a>-2时,f(x)=lnx+$\frac{a+2}{x}$的导数为f′(x)=$\frac{1}{x}$-$\frac{a+2}{{x}^{2}}$=$\frac{x-(a+2)}{{x}^{2}}$,
由f′(x)>0得x-(a+2)>0,即x>a+2,此时函数单调递增,递增区间为(a+2,+∞),
由f′(x)<0得x-(a+2)<0,即0<x<a+2,此时函数单调递减,递减区间为(0,a+2).
综上若a≤-2,则函数的单调递增区间为(0,+∞),
若a>-2,则函数的单调递增区间为(a+2,+∞),单调递减区间为(0,a+2).
点评 本题主要考查函数单调性和单调区间的求解和判断,利用函数单调性的性质以及函数单调性和导数之间的关系是解决本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
13.不等式x2+2x-3>0的解集是( )
| A. | {x|x<-3或x>1} | B. | {x|x<-1或x>3} | C. | {x|-1<x<3} | D. | {x|-3<x<1} |
8.已知下列问题:
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组;
②从甲、乙、丙三名同学中选出两名同学参加一项活动;
③从α,b,c,d四个字母中取出2个字母;
④从1,2,3,4四个数字中取出2个数字组成一个两位数.
其中是排列问题的有( )
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组;
②从甲、乙、丙三名同学中选出两名同学参加一项活动;
③从α,b,c,d四个字母中取出2个字母;
④从1,2,3,4四个数字中取出2个数字组成一个两位数.
其中是排列问题的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列两个函数相同的是( )
| A. | f(x)=lnx2,g(x)=2lnx | B. | f(x)=x,g(x)=($\sqrt{x}$)2 | ||
| C. | f(x)=cosx•tanx,g(x)=sinx | D. | f(x)=x2,g(x)=$\sqrt{{x}^{4}}$ |
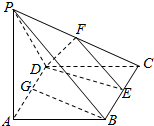 如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,
如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,