题目内容
设实数数列{an}的前n项和Sn满足Sn+1=an+1Sn(n∈ N*)。
(1)若a1,S2,-2a2成等比数列,求S2和a3;
(2)求证:对k≥3有0≤ak+1≤ak≤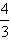 。
。
(1)若a1,S2,-2a2成等比数列,求S2和a3;
(2)求证:对k≥3有0≤ak+1≤ak≤
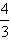 。
。解:(1)由题意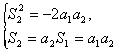
得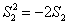
由S2是等比中项知S2≠0
因此S2=-2
由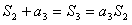
解得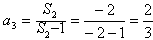 。
。
(2)由题设条件有
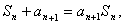
故Sn≠1,an+1≠1且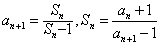
从而对k≥3有
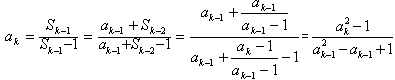 ①
①
因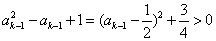 且
且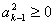 ,由①得ak≥0
,由①得ak≥0
要证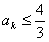
由①只要证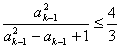
即证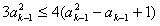
即(ak-1-2)2≥0,此式明显成立
因此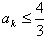 (k≥3)
(k≥3)
最后证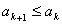
若不然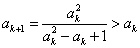
又因ak≥0,故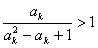
即(ak-1)2<0,矛盾
因此ak+1≤ak(k≥3)。
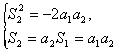
得
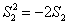
由S2是等比中项知S2≠0
因此S2=-2
由
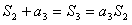
解得
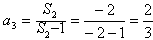 。
。(2)由题设条件有
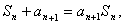
故Sn≠1,an+1≠1且
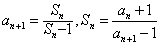
从而对k≥3有
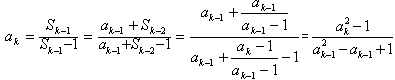 ①
①因
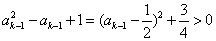 且
且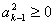 ,由①得ak≥0
,由①得ak≥0要证
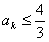
由①只要证
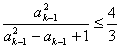
即证
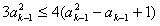
即(ak-1-2)2≥0,此式明显成立
因此
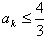 (k≥3)
(k≥3)最后证
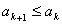
若不然
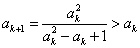
又因ak≥0,故
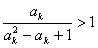
即(ak-1)2<0,矛盾
因此ak+1≤ak(k≥3)。

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 .
. .
.