题目内容
定义在R上的奇函数f(x),满足条件:在x∈(0,1)时,f(x)=
,且f(-1)=f(1).
(1)求f(x)在[-1,1]上的解析式;
(2)求f(x)在(0,1)上的取值范围;
(3)若x∈(0,1),解关于x的不等式f(x)>λ.
| 2x |
| 4x+1 |
(1)求f(x)在[-1,1]上的解析式;
(2)求f(x)在(0,1)上的取值范围;
(3)若x∈(0,1),解关于x的不等式f(x)>λ.
考点:指数函数综合题
专题:综合题,函数的性质及应用,不等式的解法及应用
分析:(1)设x∈(-1,0),则-x∈(0,1),由已知表达式可求f(-x),由奇偶性可得f(x)=-f(-x),由奇偶性可求f(±1);
(2)当x∈(0,1)时,f(x)=
,令t=2x,则t∈(1,2),利用导数可判断新函数的单调性,由单调性可求函数的取值范围;
(3)当x∈(0,1)时,令t=2x,则t∈(1,2),f(x)>λ化为
>λ,根据f(x)的范围分三种情况对λ进行讨论,借助单调性可解不等式;
(2)当x∈(0,1)时,f(x)=
| 2x |
| 4x+1 |
(3)当x∈(0,1)时,令t=2x,则t∈(1,2),f(x)>λ化为
| t |
| t2+1 |
解答:
解:(1)设x∈(-1,0),则-x∈(0,1),
又x∈(0,1)时,f(x)=
,
∴f(-x)=
=
,
∵在R上的函数f(x)为奇函数,
∴f(-x)=-f(x),
∴f(x)=-
,
f(x)在(-1,0)上的解析式为f(x)=-
.
f(-1)=f(1),即-f(1)=f(1),∴f(1)=f(-1)=0.
综上,f(x)=
.
(2)当x∈(0,1)时,f(x)=
,
令t=2x,则t∈(1,2),
函数变为y=
,y′=
<0,
∴y=
在(1,2)上为减函数,
t=1时,ymax=
;t=2时,ymin=
.
∴f(x)在(0,1)上的取值范围是(
,
).
(3)当x∈(0,1)时,令t=2x,则t∈(1,2),
f(x)>λ化为
>λ,
由(2)知
的取值范围是(
,
).
当λ≤
时t∈(1,2),x∈(0,1);
当λ≥
时,为∅;
当
<λ<
时,令
=λ,解得t=
或t=
(舍去),
又y=
在(1,2)上为减函数,
∴由
>λ得1<t<
,即1<2x<
,解得0<x<log2
;
综上所述,当λ≤
时不等式的解集为(0,1);当λ≥
时不等式的解集为∅;当
<λ<
时,不等式的解集为(0,log2
).
又x∈(0,1)时,f(x)=
| 2x |
| 4x+1 |
∴f(-x)=
| 2-x |
| 4-x+1 |
| 2x |
| 1+4x |
∵在R上的函数f(x)为奇函数,
∴f(-x)=-f(x),
∴f(x)=-
| 2x |
| 1+4x |
f(x)在(-1,0)上的解析式为f(x)=-
| 2x |
| 1+4x |
f(-1)=f(1),即-f(1)=f(1),∴f(1)=f(-1)=0.
综上,f(x)=
|
(2)当x∈(0,1)时,f(x)=
| 2x |
| 4x+1 |
令t=2x,则t∈(1,2),
函数变为y=
| t |
| t2+1 |
| 1-t2 |
| (t2+1)2 |
∴y=
| t |
| t2+1 |
t=1时,ymax=
| 1 |
| 2 |
| 2 |
| 5 |
∴f(x)在(0,1)上的取值范围是(
| 2 |
| 5 |
| 1 |
| 2 |
(3)当x∈(0,1)时,令t=2x,则t∈(1,2),
f(x)>λ化为
| t |
| t2+1 |
由(2)知
| t |
| t2+1 |
| 2 |
| 5 |
| 1 |
| 2 |
当λ≤
| 2 |
| 5 |
当λ≥
| 1 |
| 2 |
当
| 2 |
| 5 |
| 1 |
| 2 |
| t |
| t2+1 |
1+
| ||
| 2λ |
1-
| ||
| 2λ |
又y=
| t |
| t2+1 |
∴由
| t |
| t2+1 |
1+
| ||
| 2λ |
1+
| ||
| 2λ |
1+
| ||
| 2λ |
综上所述,当λ≤
| 2 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 2 |
1+
| ||
| 2λ |
点评:该题考查指数函数与其它函数的综合问题,考查函数解析式、值域的求解和不等式的解法,考查学生综合解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设i为虚数单位,则复数z=
在复平面对应的点位于( )
| 1-2i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知直线l的参数方程为
(t为参数),则直线l的普通方程为( )
|
| A、x-y-2=0 |
| B、x-y+2=0 |
| C、x+y=0 |
| D、x+y-2=0 |
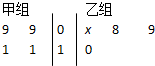 如图,茎叶图记录了甲、乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.若甲、乙两组共有8名同学植树棵数的平均数为9,则x为( )
如图,茎叶图记录了甲、乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.若甲、乙两组共有8名同学植树棵数的平均数为9,则x为( )