题目内容
11.已知cos(2α-β)=-$\frac{11}{14}$,sin(α-2β)=$\frac{4\sqrt{3}}{7}$,0<β<$\frac{π}{4}$<α<$\frac{π}{2}$,则α+β=$\frac{π}{3}$.分析 根据两角和差的余弦公式先求出cos(α+β)的值,然后判断角的范围进行求解即可.
解答 解:∵α+β=2α-β-(α-2β),
∴cos(α+β)=cos[2α-β-(α-2β)]=cos(2α-β)cos(α-2β)+sin(2α-β)sin(α-2β),
∵0<β<$\frac{π}{4}$<α<$\frac{π}{2}$,
∴0<2β<$\frac{π}{2}$<2α<π,
0>-β>-$\frac{π}{4}$>-α>-$\frac{π}{2}$,
则$\frac{π}{4}$<2α-β<π,-$\frac{π}{4}$<α-2β<$\frac{π}{2}$,
∵cos(2α-β)=-$\frac{11}{14}$,∴sin(2α-β)=$\frac{5\sqrt{3}}{14}$,
∵sin(α-2β)=$\frac{4\sqrt{3}}{7}$,∴cos(α-2β)=$\frac{1}{7}$,
则cos(α+β)=cos[2α-β-(α-2β)]=cos(2α-β)cos(α-2β)+sin(2α-β)sin(α-2β)
=-$\frac{11}{14}$×$\frac{1}{7}$+$\frac{5\sqrt{3}}{14}$×$\frac{4\sqrt{3}}{7}$=$\frac{-11+60}{98}$=$\frac{49}{98}$=$\frac{1}{2}$,
∵0<β<$\frac{π}{4}$<α<$\frac{π}{2}$,
∴0<β<$\frac{π}{4}$,$\frac{π}{4}$<α<$\frac{π}{2}$,
则$\frac{π}{4}$<α+β<$\frac{3π}{4}$,
∴α+β=$\frac{π}{3}$或$\frac{2π}{3}$,
∵cos(2α-β)=-$\frac{11}{14}$<0,∴$\frac{π}{2}$<2α-β<π,
∵sin(α-2β)=$\frac{4\sqrt{3}}{7}$∈($\frac{\sqrt{3}}{2}$,1),∴$\frac{π}{3}$<α-2β<$\frac{π}{2}$
-$\frac{π}{2}$<2β-α<-$\frac{π}{3}$,
则0<α+β<$\frac{2π}{3}$.,
∴α+β=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$
点评 本题主要考查三角函数的化简和求解,利用拆角技巧,结合两角和差的余弦公式进行求解是解决本题的关键.

| A. | y=x+1 | B. | y=-$\frac{1}{x}$ | C. | y=-x|x| | D. | y=2x-2-x |
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{2},0)$ | C. | (0,1) | D. | (1,0) |
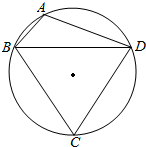 某城市在进行规划时,准备设计一个圆形的开放式公园,为达到社会和经济效益双丰收,园林公司进行如下设计,安排圆内接四边形ABCD作为绿化区域,其余作为市民活动区域,其中△ABD区域种植花木后出售,△BCD区域种植草皮后出售,已知草皮每平方米售价为a元,花木每平方米的售价是草皮每平方米售价的三倍,若BC=6km,AD=CD=4km.
某城市在进行规划时,准备设计一个圆形的开放式公园,为达到社会和经济效益双丰收,园林公司进行如下设计,安排圆内接四边形ABCD作为绿化区域,其余作为市民活动区域,其中△ABD区域种植花木后出售,△BCD区域种植草皮后出售,已知草皮每平方米售价为a元,花木每平方米的售价是草皮每平方米售价的三倍,若BC=6km,AD=CD=4km.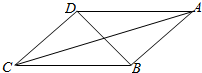 如图,在平行四边形ABCD中,已知AB=CD=a,AD=2a,∠DAB=60°,AC∩BD=E,将其沿对角线BD折成直二面角.
如图,在平行四边形ABCD中,已知AB=CD=a,AD=2a,∠DAB=60°,AC∩BD=E,将其沿对角线BD折成直二面角.