Question

1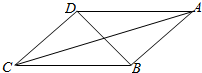．如图，在平行四边形ABCD中，已知AB=CD=a，AD=2a，∠DAB=60°，AC∩BD=E，将其沿对角线BD折成直二面角．
（1）证明：AB⊥平面BCD；
（2）证明：平面ACD⊥平面ABD．

Answer 1

分析 （1）取BC中点M、AD中点N，连结NB、DM，推导出四边形BNDM是菱形，由此能证明AB⊥平面BCD．
（2）由ME是△BCD中位线，得CD⊥BD，由平面BCD⊥平面ABD，得CD⊥平面ABD，由此能证明平面ACD⊥平面ABD．

解答 证明：（1）取BC中点M、AD中点N，连结NB、DM，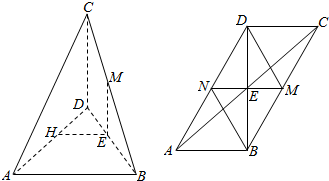
AN=$\frac{AD}{2}$=a，AN=AB，∠NAB=60°，
∴△BAN是等边三角形，AN=BN，
同理CD=DM，∴四边形BNDM是菱形，
∵MN是菱形对角线，∴BD⊥MN，
∴∠MEN是二面角A-BD-C的平面角，∴∠MEN=90°，
∵NE⊥BD，∴NE⊥平面BCD，
∵NE是△DAB的中位线，∴AB∥NE，
∴AB⊥平面BCD．
（2）∵M，E分别是BC、BD的中点，∴ME是△BCD中位线，
∴EM∥CD，∵EM⊥BD，∴CD⊥BD，
∵AB⊥平面BCD，AB?平面ABD，∴平面BCD⊥平面ABD，
∴CD⊥平面ABD，
∵CD?平面ACD，
∴平面ACD⊥平面ABD．

点评 本题考查线面垂直、面面垂直的证明，是中档题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．