题目内容
设a、b、c均为正数，且a＋b＋c＝1，证明：
(1)ab＋bc＋ac≤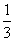
；
(2)
＋
＋
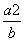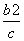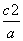≥1.
[解析] (1)由a2＋b2≥2ab，b2＋c2≥2bc，c2＋a2≥2ca得，
a2＋b2＋c2≥ab＋bc＋ca.
由题设得(a＋b＋c)2＝1，
即a2＋b2＋c2＋2ab＋2bc＋2ca＝1.
所以3(ab＋bc＋ca)≤1，即ab＋bc＋ca≤.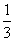
(2)因为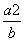＋b≥2a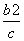，＋c≥2b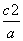，＋a≥2c，
故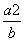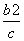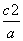＋＋＋(a＋b＋c)≥2(a＋b＋c)，
即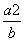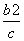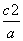＋＋≥a＋b＋c.所以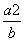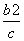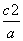＋＋≥1.
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
的值为________．
.
≥
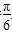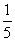|a2－a|对于x∈[2,6]恒成立，则实数a的取值范围是________．
，当且仅当
＝
时上式取等号．利用以上结论，可以得到函数f(x)＝
＋
(x∈(0，
))的最小值为________．