题目内容
已知将函数y=cos2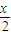 -sin2
-sin2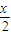 +2
+2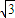 sin
sin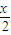 cos
cos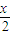 的图象上所有点向左平移
的图象上所有点向左平移 个单位,再把所得的图象上所有点得横坐标变为原来的
个单位,再把所得的图象上所有点得横坐标变为原来的 倍(纵坐标不变),得到函数f(x)的图象.
倍(纵坐标不变),得到函数f(x)的图象.(I)求函数f(x)的表达式及f(x)的最小正周期;
(II)求f(x)的单调递减区间及f(x)在区间[0,
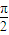 ]上的最大值和最小值.
]上的最大值和最小值.
【答案】分析:(I)由三角函数的运算公式可得:y=2sin(x+ ),由图象变换的知识可得f(x)=2sin(2x
),由图象变换的知识可得f(x)=2sin(2x ),进而可得周期;
),进而可得周期;
(II)由整体法可得函数的单调区间,进而可得函数在区间[0, ]的最值.
]的最值.
解答:解:(I)由三角函数的运算公式可得:y=cos2 -sin2
-sin2 +2
+2 sin
sin cos
cos
=cosx+ sinx=2(
sinx=2( cosx
cosx sinx)=2sin(x+
sinx)=2sin(x+ ),
),
由图象变换的知识可得将上述函数图象向左平移 个单位,横坐标变为原来的
个单位,横坐标变为原来的 倍(纵坐标不变),
倍(纵坐标不变),
所得函数为:f(x)=2sin(2x ),故其周期为:T=
),故其周期为:T= =π;
=π;
(II)由2kπ
 2kπ+
2kπ+ ,得f(x)=2sin(2x
,得f(x)=2sin(2x )的递减区间为:
)的递减区间为:
[kπ+ ,kπ+
,kπ+ ](k∈Z),又∵x∈[0,
](k∈Z),又∵x∈[0, ],∴2x
],∴2x ∈[
∈[ ,
, ],
],
∴sin(2x )∈[
)∈[ ,1],
,1],
所以当x= 时,f(x)取得最小值
时,f(x)取得最小值 ,当x=
,当x= 时,f(x)取得最大值2
时,f(x)取得最大值2
点评:本题考查三角函数的运算和图象变换,涉及区间最值的求解,属中档题.
 ),由图象变换的知识可得f(x)=2sin(2x
),由图象变换的知识可得f(x)=2sin(2x ),进而可得周期;
),进而可得周期;(II)由整体法可得函数的单调区间,进而可得函数在区间[0,
 ]的最值.
]的最值.解答:解:(I)由三角函数的运算公式可得:y=cos2
 -sin2
-sin2 +2
+2 sin
sin cos
cos
=cosx+
 sinx=2(
sinx=2( cosx
cosx sinx)=2sin(x+
sinx)=2sin(x+ ),
),由图象变换的知识可得将上述函数图象向左平移
 个单位,横坐标变为原来的
个单位,横坐标变为原来的 倍(纵坐标不变),
倍(纵坐标不变),所得函数为:f(x)=2sin(2x
 ),故其周期为:T=
),故其周期为:T= =π;
=π;(II)由2kπ

 2kπ+
2kπ+ ,得f(x)=2sin(2x
,得f(x)=2sin(2x )的递减区间为:
)的递减区间为:[kπ+
 ,kπ+
,kπ+ ](k∈Z),又∵x∈[0,
](k∈Z),又∵x∈[0, ],∴2x
],∴2x ∈[
∈[ ,
, ],
],∴sin(2x
 )∈[
)∈[ ,1],
,1],所以当x=
 时,f(x)取得最小值
时,f(x)取得最小值 ,当x=
,当x= 时,f(x)取得最大值2
时,f(x)取得最大值2点评:本题考查三角函数的运算和图象变换,涉及区间最值的求解,属中档题.

练习册系列答案
相关题目