题目内容
下列命题中,真命题的个数为( )
(1)在△ABC中,若A>B,则sinA>sin B;
(2)已知
=(3,4),
=(-2,-1),则
在
上的投影为-2;
(3)已知p:?x∈R,cosx=1,q:?R,x2-x+1>0,则“p∧¬q”为假命题
(4)要得到函数y=cos(
-
)的图象,只需将y=sin
的图象向左平移
个单位.
(1)在△ABC中,若A>B,则sinA>sin B;
(2)已知
| AB |
| CD |
| AB |
| CD |
(3)已知p:?x∈R,cosx=1,q:?R,x2-x+1>0,则“p∧¬q”为假命题
(4)要得到函数y=cos(
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
分析:对于(1)可先证充分性,由,“A>B”推导“sinA>sinB”,分A是锐角与A不是锐角两类证明即可;再证必要性,由于在(0,π)上正弦函数不是单调函数,可分两类证明,当A是钝角时,与A不是钝角时,易证,再由充分条件必要条件的定义得出正确选项即可;
对于(2)先求得向量的坐标,再求得其数量积和模,然后用投影公式求解.判断即可.
对于(3)分别判断两个命题的正误,进而根据复合命题真假判断的真值表,可判断其正误
对于(4)求出将y=sin
的图象向左平移
个单位后函数的解析式,比照后可得到结论
对于(2)先求得向量的坐标,再求得其数量积和模,然后用投影公式求解.判断即可.
对于(3)分别判断两个命题的正误,进而根据复合命题真假判断的真值表,可判断其正误
对于(4)求出将y=sin
| x |
| 2 |
| π |
| 4 |
解答:解:(1)由题意,在△ABC中,“A>B”,由于A+B<π,必有B<π-A
若A,B都是锐角,显然有“sinA>sinB”成立,
若A,B之一为锐角,必是B为锐角,此时有π-A不是钝角,由于A+B<π,必有B<π-A≤
,此时有sin(π-A)=sinA>sinB
综上,△ABC中,“A>B”是“sinA>sinB”成立的充分条件;
当sinA>sinB时,若A不是锐角,显然可得出A>B,若A是锐角,亦可得出A>B,
综上在△ABC中,“A>B”是“sinA>sinB”成立的必要条件
综合1°,2°知,在△ABC中,“A>B”是“sinA>sinB”成立的充要条件,
本选项正确;
(2)已知
=(3,4),
=(-2,-1),|
|=5,|
|=
,
cosα=
=
≠-2,则
在
上的投影为-2,不正确.
(3)p:?x=0∈R,cosx=1,正确;q:?x∈R,x2-x+1=(x-
)2+
>0,正确,所以¬q不正确,则“p∧¬q”为假命题,正确.
(4)函数y=sin
的图象向左平移
个单位得到函数y=sin
=sin(
+
)的图象,而y=sin(
+
)和y=cos(
-
)不是同一个函数
故选B.
若A,B都是锐角,显然有“sinA>sinB”成立,
若A,B之一为锐角,必是B为锐角,此时有π-A不是钝角,由于A+B<π,必有B<π-A≤
| π |
| 2 |
综上,△ABC中,“A>B”是“sinA>sinB”成立的充分条件;
当sinA>sinB时,若A不是锐角,显然可得出A>B,若A是锐角,亦可得出A>B,
综上在△ABC中,“A>B”是“sinA>sinB”成立的必要条件
综合1°,2°知,在△ABC中,“A>B”是“sinA>sinB”成立的充要条件,
本选项正确;
(2)已知
| AB |
| CD |
| AB |
| CD |
| 5 |
| AB |
| ||||
|
|
| -10 | ||
|
| AB |
| CD |
(3)p:?x=0∈R,cosx=1,正确;q:?x∈R,x2-x+1=(x-
| 1 |
| 2 |
| 3 |
| 4 |
(4)函数y=sin
| x |
| 2 |
| π |
| 4 |
x+
| ||
| 2 |
| x |
| 2 |
| π |
| 8 |
| x |
| 2 |
| π |
| 8 |
| x |
| 2 |
| π |
| 4 |
故选B.
点评:本题考查命题的正误,向量的数量积的应用,三角函数的对称轴的应用,考查基本知识的灵活运用.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
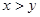 ,则
,则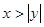 ”的逆命题
”的逆命题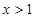 ,则
,则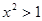 ”的否命题
”的否命题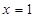 ,则
,则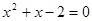 ”的否命题
”的否命题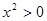 ,则
,则