题目内容
2.从装有若干个大小相同的红球、白球和黄球的袋中随机摸出1个球,摸到红球、白球和黄球的概率分别为$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$,从袋中随机摸出一个球,记下颜色后放回,连续摸3次,则记下的颜色中有红有白但没有黄的概率为( )| A. | $\frac{5}{36}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{12}$ | D. | $\frac{1}{2}$ |
分析 记下的颜色中有红有白但没有黄的情况有两种:2红1白,1红2白,由此能求出所求概率.
解答 解:∵从装有若干个大小相同的红球、白球和黄球的袋中随机摸出1个球,
摸到红球、白球和黄球的概率分别为$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{6}$,
从袋中随机摸出一个球,记下颜色后放回,连续摸3次,
∴记下的颜色中有红有白但没有黄的情况有两种:2红1白,1红2白,
则所求概率:
p=${C}_{3}^{1}×\frac{1}{2}×(\frac{1}{3})^{2}+{C}_{3}^{2}(\frac{1}{2})^{2}×\frac{1}{3}$=$\frac{5}{12}$.
故选:C.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.

练习册系列答案
相关题目
13.已知集合A={x|x2-x-2≤0,x∈R},B={x|lg(x+1)<1,x∈Z},则A∩B=( )
| A. | (0,2) | B. | [0,2] | C. | {0,2} | D. | {0,1,2} |
17.在等差数列{an}中,a3-a2=-2,a7=-2,则a9=( )
| A. | 2 | B. | -2 | C. | -4 | D. | -6 |
7. 阅读如图所示的程序框图,若输出的结果是63,则判断框内n的值可为( )
阅读如图所示的程序框图,若输出的结果是63,则判断框内n的值可为( )
 阅读如图所示的程序框图,若输出的结果是63,则判断框内n的值可为( )
阅读如图所示的程序框图,若输出的结果是63,则判断框内n的值可为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
14.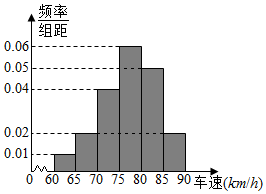 对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )
对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )
 对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )
对高速公路某段上汽车行驶速度进行抽样调查,画出如图频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h的概率( )| A. | 75,0.25 | B. | 80,0.35 | C. | 77.5,0.25 | D. | 77.5,0.35 |
11.已知集合A={x|x≥4},B={x|-1≤2x-1≤0},则∁RA∩B=( )
| A. | (4,+∞) | B. | [0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,4) | D. | (1,4] |
12.已知A={-2,-1,0,1,2},B={x|2x-1>0},则A∩B=( )
| A. | {-2,-1,0,1,2} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |