题目内容
1.已知球O的直径PQ=4,A、B、C是球O球面上的三点,△ABC是等腰直角三角形,且∠ACB=90°,∠APQ=∠BPQ=∠CPQ=30°,则三棱锥P-ABC的体积为( )| A. | $\frac{3\sqrt{3}}{4}$ | B. | 3 | C. | $\frac{3\sqrt{3}}{2}$ | D. | 6 |
分析 P在面ABC的投影O是△ABC的外心,且为球心,求出AB=2$\sqrt{3}$,AC=BC=$\sqrt{6}$,计算出锥体的体积即可.
解答 解:∵△ABC是等腰直角三角形,∠APQ=∠BPQ=∠CPQ=30°
∴P在面ABC的投影O是△ABC的外心,且为球心,
∵PQ是直径,
∴∠PCQ=90°.
∴PC=4cos30°=2$\sqrt{3}$,
∴PO=2$\sqrt{3}$•cos30°=3.
OC=2$\sqrt{3}$sin30°=$\sqrt{3}$
∴AB=2$\sqrt{3}$,AC=BC=$\sqrt{6}$.
三棱锥P-ABC体积=$\frac{1}{3}$PO•S△ABC=$\frac{1}{3}$×$\frac{1}{2}$×$\sqrt{6}$×$\sqrt{6}$×3=3.
故选:B.
点评 本题主要考查三棱锥的体积公式的计算,考查学生的运算能力,利用三棱锥和球的关系是解决本题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
13.若椭圆和双曲线C:2x2-2y2=1有相同的焦点,且该椭圆经过点$({1,-\frac{3}{2}})$,则椭圆的方程为( )
| A. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{5}=1$ | D. | $\frac{x^2}{9}+\frac{y^2}{5}=1$ |
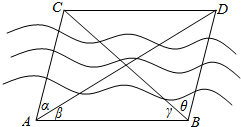 如图,为测不可到达的河北岸C,D两点间的距离,在河南岸选取A,B两点,测得AB=100m,α=β=30°,γ=45°,θ=75°,试求C,D间的距离.
如图,为测不可到达的河北岸C,D两点间的距离,在河南岸选取A,B两点,测得AB=100m,α=β=30°,γ=45°,θ=75°,试求C,D间的距离.