题目内容
7.在平面直角坐标系xOy中,已知△ABC的顶点B(-5,0)和C(5,0),顶点A在双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的右支上,则$\frac{sinC-sinB}{sinA}$=$\frac{3}{5}$?.分析 首先由正弦定理,有$\frac{sinC-sinB}{sinA}$=$\frac{AB-AC}{BC}$,进而根据双曲线的几何性质,可得|CB|=2c=4,|AB|-|CA|=2a=6,代入$\frac{AB-AC}{BC}$,即可得到答案.
解答 解:根据正弦定理:在△ABC中,有$\frac{sinC-sinB}{sinA}$=$\frac{AB-AC}{BC}$,
又由题意C、B分别是双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的左、右焦点,
则|CB|=2c=10,
且△ABC的顶点A在双曲线的右支上,
又可得|AB|-|AC|=2a=6,
则$\frac{sinC-sinB}{sinA}$=$\frac{AB-AC}{BC}$=$\frac{6}{10}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查双曲线的定义、方程和性质,注意运用定义法,以及正弦定理的应用,考查计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知全集为R,集合A={x|$\frac{x-1}{x}$<0},B={x|x≥1},则A∪B等于( )
| A. | {x|x>0} | B. | {x|0<x<1} | C. | {x|x<1} | D. | {x|x≤0} |
16.函数f(x)=3x-($\frac{1}{2}$)x的零点存在区间为( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
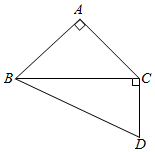 如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.
如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.