题目内容
已知函数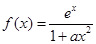 ,其中
,其中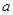 为正实数,
为正实数,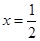 是
是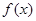 的一个极值点.
的一个极值点.
(Ⅰ)求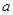 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数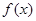 在
在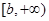 上的最小值.
上的最小值.
(Ⅰ)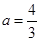 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)由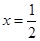 为函数
为函数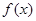 的一个极值点,得到
的一个极值点,得到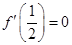 便可求出
便可求出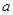 的值,但在求得答案后注意
的值,但在求得答案后注意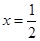 处附近左、右两侧导数符号相反,即成为极值点的必要性;(Ⅱ)对于含参函数的最值问题,一般结合导数考察函数在相应区间的单调性,利用端点值以及函数的极值确定函数的最小值.
处附近左、右两侧导数符号相反,即成为极值点的必要性;(Ⅱ)对于含参函数的最值问题,一般结合导数考察函数在相应区间的单调性,利用端点值以及函数的极值确定函数的最小值.
试题解析: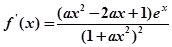
(Ⅰ)因为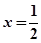 是函数
是函数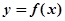 的一个极值点,
的一个极值点,
所以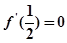 ,因此,
,因此,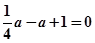 ,解得
,解得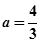 ,
,
经检验,当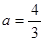 时,
时,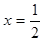 是
是 的一个极值点,故所求
的一个极值点,故所求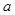 的值为
的值为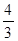 .
.
4分
(Ⅱ)由(Ⅰ)可知,
令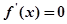 ,得
,得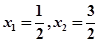
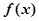 与
与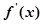 的变化情况如下:
的变化情况如下:

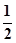


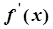
+ 0 - 0 + 



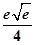
 练习册系列答案
练习册系列答案
全品高考短平快系列答案
初中学业会考仿真卷系列答案
初中总复习全优设计系列答案
全国名师点拨小学毕业系统总复习系列答案
中考试题分类精华卷系列答案

名校密卷小升初模拟试卷系列答案
68所名校图书小学毕业升学必做的16套试卷系列答案
高分计划初中文言文提分训练系列答案
夺冠百分百中考试题调研系列答案
相关题目
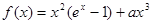
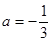 时,求
时,求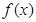 的单调区间;
的单调区间;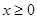 时,
时,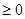 恒成立,求
恒成立,求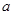 的取值范围.
的取值范围. .
. 时,求
时,求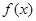 在
在 最小值;
最小值; 的取值范围;
的取值范围; (
( ).
). 是实数,函数
是实数,函数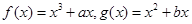 ,
, 和
和 ,分别是
,分别是 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 ,若函数
,若函数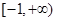 上单调性一致,求实数
上单调性一致,求实数 的取值范围;
的取值范围; 且
且 ,若函数
,若函数 的最大值.
的最大值. .
. 时,求函数
时,求函数 的单调增区间;
的单调增区间; 上的最小值.
上的最小值. ,
,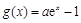 (其中
(其中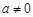 ,
,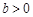 ),且函数
),且函数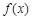 的图象在点
的图象在点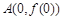 处的切线与函数
处的切线与函数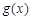 的图象在点
的图象在点 处的切线重合.
处的切线重合.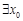 ,满足
,满足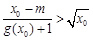 ,求实数
,求实数 的取值范围;
的取值范围;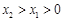 ,试探究
,试探究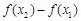 与
与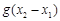 的大小,并说明你的理由.
的大小,并说明你的理由. (
( ).
). 时,求函数
时,求函数 的极值;
的极值;  ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
, 取得极值,求实数
取得极值,求实数 的值;
的值; 时,求
时,求 上的最小值;
上的最小值; ,直线
,直线 都不是曲线
都不是曲线 的切线,求实数
的切线,求实数 在点
在点 处取得极小值-4,使其导数
处取得极小值-4,使其导数 的
的 的取值范围为
的取值范围为 ,求:
,求: 的解析式;
的解析式;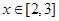 ,求
,求 的最大值;
的最大值;