题目内容
已知函数 ,
,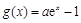 (其中
(其中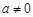 ,
,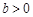 ),且函数
),且函数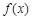 的图象在点
的图象在点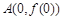 处的切线与函数
处的切线与函数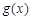 的图象在点
的图象在点 处的切线重合.
处的切线重合.
(Ⅰ)求实数a,b的值;
(Ⅱ)若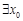 ,满足
,满足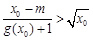 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅲ)若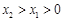 ,试探究
,试探究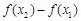 与
与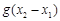 的大小,并说明你的理由.
的大小,并说明你的理由.
(Ⅰ) ,
,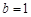 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ) .
.
解析试题分析:(Ⅰ)先求出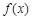 在点
在点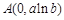 处切线方程为
处切线方程为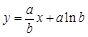 ,再求出
,再求出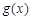 在点
在点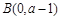 处切线方程为
处切线方程为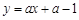 ,比较两方程的系数即可得
,比较两方程的系数即可得 ,
,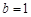 ;(Ⅱ)根据题意可转化成
;(Ⅱ)根据题意可转化成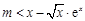 在
在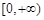 上有解,令
上有解,令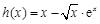 ,只需
,只需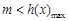 ,分类讨论可求得实数m的取值范围是
,分类讨论可求得实数m的取值范围是 ;
;
(Ⅲ)令 ,再证函数
,再证函数 在区间
在区间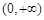 上单调递增,当
上单调递增,当 时,
时, 恒成立,即可得对任意
恒成立,即可得对任意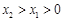 ,有
,有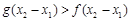 ,再证
,再证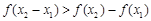 即可得证.
即可得证.
试题解析:(Ⅰ)∵ ,∴
,∴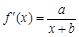 ,则
,则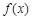 在点
在点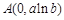 处切线的斜率
处切线的斜率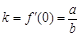 ,切点
,切点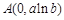 ,则
,则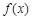 在点
在点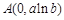 处切线方程为
处切线方程为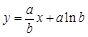 ,
,
又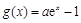 ,∴
,∴ ,则
,则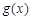 在点
在点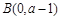 处切线的斜率
处切线的斜率 ,切点
,切点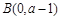 ,则
,则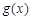 在点
在点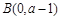 处切线方程为
处切线方程为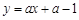 ,
,
由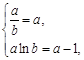 解得
解得 ,
,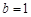 . 4分
. 4分
(Ⅱ)由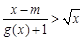 得
得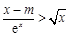 ,故
,故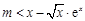 在
在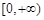 上有解,
上有解,
令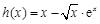 ,只需
,只需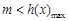 . 6分
. 6分
①当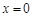 时,
时,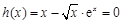 ,所以
,所以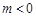 ; 7分
; 7分
②当 时,∵
时,∵ ,
,
∵ ,∴
,∴ ,
,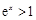 ,∴
,∴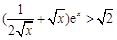 ,
,
故 ,即函数
,即函数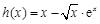 在区间
在区间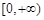 上单调递减,
上单调递减,
所以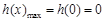 ,此时
,此时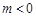 .
.
综合①②得实数m的取值范围是 . 9分
. 9分
(Ⅲ)令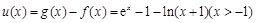 ,
,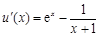
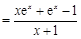 .
.
令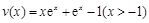 ,则
,则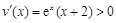 在
在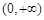 上恒成立,
上恒成立,
∴当 时,
时, 成立,∴
成立,∴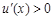 在
在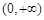 上恒成立,
上恒成立,
故函数 在区间
在区间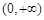 上单调递增,∴当
上单调递增,∴当 时,
时, 恒成立,
恒成立,
故对于任意

练习册系列答案
相关题目
 ,
,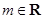 .
.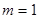 时,求曲线
时,求曲线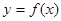 在点
在点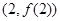 处的切线方程;
处的切线方程;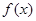 在区间
在区间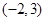 上是减函数,求
上是减函数,求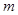 的取值范围.
的取值范围. .
.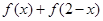 的值是否为定值?若是,求出该定值;若不是,请说明理由;
的值是否为定值?若是,求出该定值;若不是,请说明理由;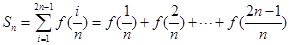 ,其中
,其中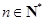 ,求
,求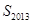 ;
;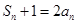 .若不等式
.若不等式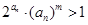 对
对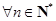 且
且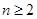 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
.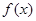 的单调区间;
的单调区间;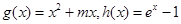 ,若在
,若在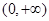 上至少存在一点
上至少存在一点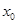 ,使得
,使得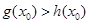 成立,求
成立,求 的范围.
的范围.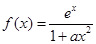 ,其中
,其中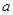 为正实数,
为正实数,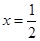 是
是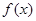 的一个极值点.
的一个极值点. 时,求函数
时,求函数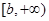 上的最小值.
上的最小值.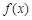 是定义在
是定义在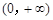 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记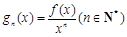 .若对定义域内的每一个
.若对定义域内的每一个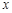 ,总有
,总有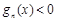 ,则称
,则称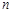 阶负函数”;若对定义域内的每一个
阶负函数”;若对定义域内的每一个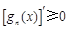 ,
,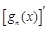 为函数
为函数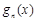 的导函数).
的导函数). 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数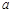 的取值范围;
的取值范围;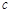 ,使得
,使得 恒成立,试判断
恒成立,试判断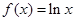 ,
,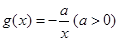
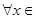 (0,e],都有f(x)≥g(x)+
(0,e],都有f(x)≥g(x)+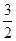 ,求实数a的取值范围.
,求实数a的取值范围.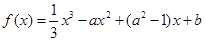 (
(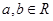 ),其图像在点(1,
),其图像在点(1,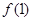 )处的切线方程为
)处的切线方程为 .
.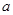 ,
,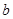 的值;
的值;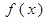 的单调区间和极值;
的单调区间和极值;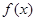 在区间[-2,5]上的最大值.
在区间[-2,5]上的最大值.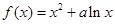 的图象在点
的图象在点 处的切线斜率为
处的切线斜率为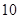 .
.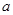 的值;
的值;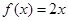 根的个数,证明你的结论;
根的个数,证明你的结论; ,使得曲线
,使得曲线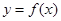 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.