题目内容
【题目】已知椭圆![]() :
:![]() ,其中
,其中![]() ,点
,点![]() 是椭圆
是椭圆![]() 的右顶点,射线
的右顶点,射线![]() :
:![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)设椭圆![]() 的长半轴、短半轴的长分别为
的长半轴、短半轴的长分别为![]() 、
、![]() ,当
,当![]() 的值在区间
的值在区间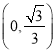 中变化时,求
中变化时,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,以![]() 为焦点,
为焦点,![]() 为顶点且开口方向向左的抛物线过点
为顶点且开口方向向左的抛物线过点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)联立方程组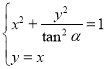 ,再求解即可;
,再求解即可;
(2)由椭圆的几何性质可得![]() ,
,![]() ,再解不等式
,再解不等式 即可;
即可;
(3)先求出抛物线的方程为![]() ,由点
,由点![]() 在抛物线上可得
在抛物线上可得![]() ,再令
,再令![]() ,则
,则![]() ①,其中
①,其中![]() ,则问题可转化为抛物线①在区间
,则问题可转化为抛物线①在区间![]() 上与椭圆有一个交点的充要条件是:
上与椭圆有一个交点的充要条件是: ,再求解即可.
,再求解即可.
解:(1)解方程组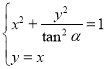 ,
,
得![]() ,
,
所以![]() ;
;
(2)因为![]() ,
,![]() ,所以椭圆的焦点在
,所以椭圆的焦点在![]() 轴上,
轴上,![]() ,
,![]() ,
,
由条件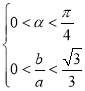 ,得:
,得: ,所以
,所以![]() ;
;
(3)由题意得:![]() ,且抛物线焦点
,且抛物线焦点![]() 与顶点
与顶点![]() 的距离为
的距离为![]() ,
,
设抛物线方程为:![]() ,那么
,那么![]() ,
,
故抛物线的方程为![]() ,
,
因为点![]() 在抛物线上,所以
在抛物线上,所以![]() ,
,
![]() ,
,
设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
令![]() ①,其中
①,其中![]() ,
,
抛物线①开口向上,其对称轴![]() ,
,
抛物线①在区间![]() 上与椭圆有一个交点的充要条件是:
上与椭圆有一个交点的充要条件是: ,
,
即 ,所以
,所以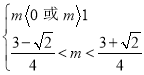 ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目