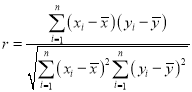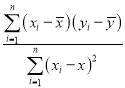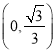题目内容
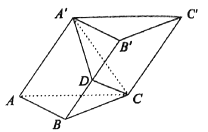
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() ,
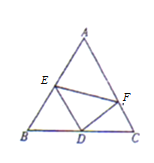
,![]() 分别为
分别为![]() ,
,![]() 边的中点,以
边的中点,以![]() 为折痕把
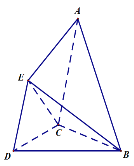
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() ..
..
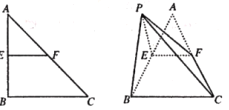
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 为线段
为线段![]() 上动点,求直线
上动点,求直线![]() 与平面
与平面![]() 所成角的正弦值的最大值.
所成角的正弦值的最大值.
【答案】(Ⅰ)见解析;
(Ⅱ)![]() .
.
【解析】
(Ⅰ)由题,易证得![]() ,即可证得结论;
,即可证得结论;
(Ⅱ)取BE的中点O,连接PO,易证得PO![]() ,然后以O为原点,建立直角坐标系,利用空间向量求得
,然后以O为原点,建立直角坐标系,利用空间向量求得![]() 与平面
与平面![]() 所成角的正弦值,求得其最大值即可.
所成角的正弦值,求得其最大值即可.
(Ⅰ)E,F分别为AB ,AC边的中点,所以![]()
因为![]()
![]()
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)取BE的中点O,连接PO,
由(1)知![]() 平面
平面![]() ,EF
,EF![]() 平面BCFE,,
平面BCFE,,
所以平面PBE![]() 平面BCFE
平面BCFE
因为PB=BE=PE,所以PO![]() ,
,
又因为PO![]() 平面PBE,平面PBE
平面PBE,平面PBE![]() 平面BCFE=BE
平面BCFE=BE
所以PO![]() .
.
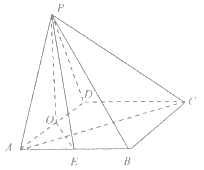
过O作OM//BC交CF于M,分别以OB,OM,OP所在直线为
x,y,z轴建立空间直角坐标系,如图所示.
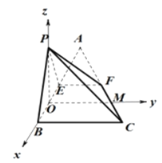
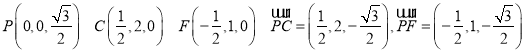
N为线段PF上一动点设![]() ,由,
,由,![]()
得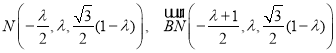
设平面PCF的法向量为![]()
则 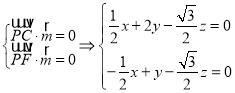 即取
即取 ![]()
设直线BN与平面PCF所成角![]()
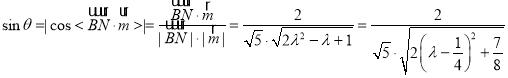
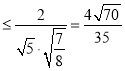
直线BN与平面PCF所成角的正弦值的最大值为![]()

 优学名师名题系列答案
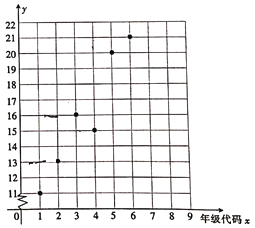
优学名师名题系列答案【题目】某公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x与乘客等候人数y之间的关系,经过调查得到如下数据:
间隔时间x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
(1)从这6组数据中随机选取4组数据,求剩下的2组数据的间隔时间相邻的概率;
(2)若选取的是中间4组数据,求y关于x的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”.
,并判断此方程是否是“恰当回归方程”.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: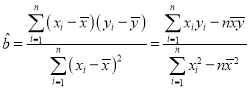 ,
,![]() .
.