题目内容
设f(x)是R上的奇函数,且当x∈(0,+∞)时,f(x)=x(1-
),则f(0)= ;f(-8)= .
| 3 | x |
考点:函数的值
专题:函数的性质及应用
分析:由奇函数的性质得f(0)=0;f(-8)=-f(8)=-8(1-
)=8.
| 3 | 8 |
解答:
解:∵f(x)是R上的奇函数,
且当x∈(0,+∞)时,f(x)=x(1-
),
∴f(0)=0;
f(-8)=-f(8)=-8(1-
)=8.
故答案为:0;8.
且当x∈(0,+∞)时,f(x)=x(1-
| 3 | x |
∴f(0)=0;
f(-8)=-f(8)=-8(1-
| 3 | 8 |
故答案为:0;8.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=f(-x)的图象与函数y=f(4+x)的图象关于( )
| A、x=4对称 |
| B、x=-4对称 |
| C、x=2对称 |
| D、x=-2对称 |
已知数列{an}满足a1=3,an+1=
(n∈N*),Tn为数列{an}的前n项之积,则T2010=( )
| an-1 |
| an+1 |
A、
| ||
B、-
| ||
C、
| ||
| D、-6 |
已知定义在R上的偶函数f(x)满足f(x-1)=f(x+1),当0≤x≤1时,f(x)=x2,如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为( )
| A、2k(k∈Z) | ||
B、2k-
| ||
C、2K或2K+
| ||
D、2K或2K-
|
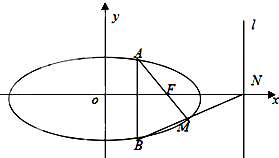 如图,已知直线x+ky-1=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为3.
如图,已知直线x+ky-1=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为3.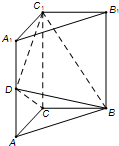 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=